可观测量的期望值如何计算,期望值在量子力学中代表什么?
参考资料
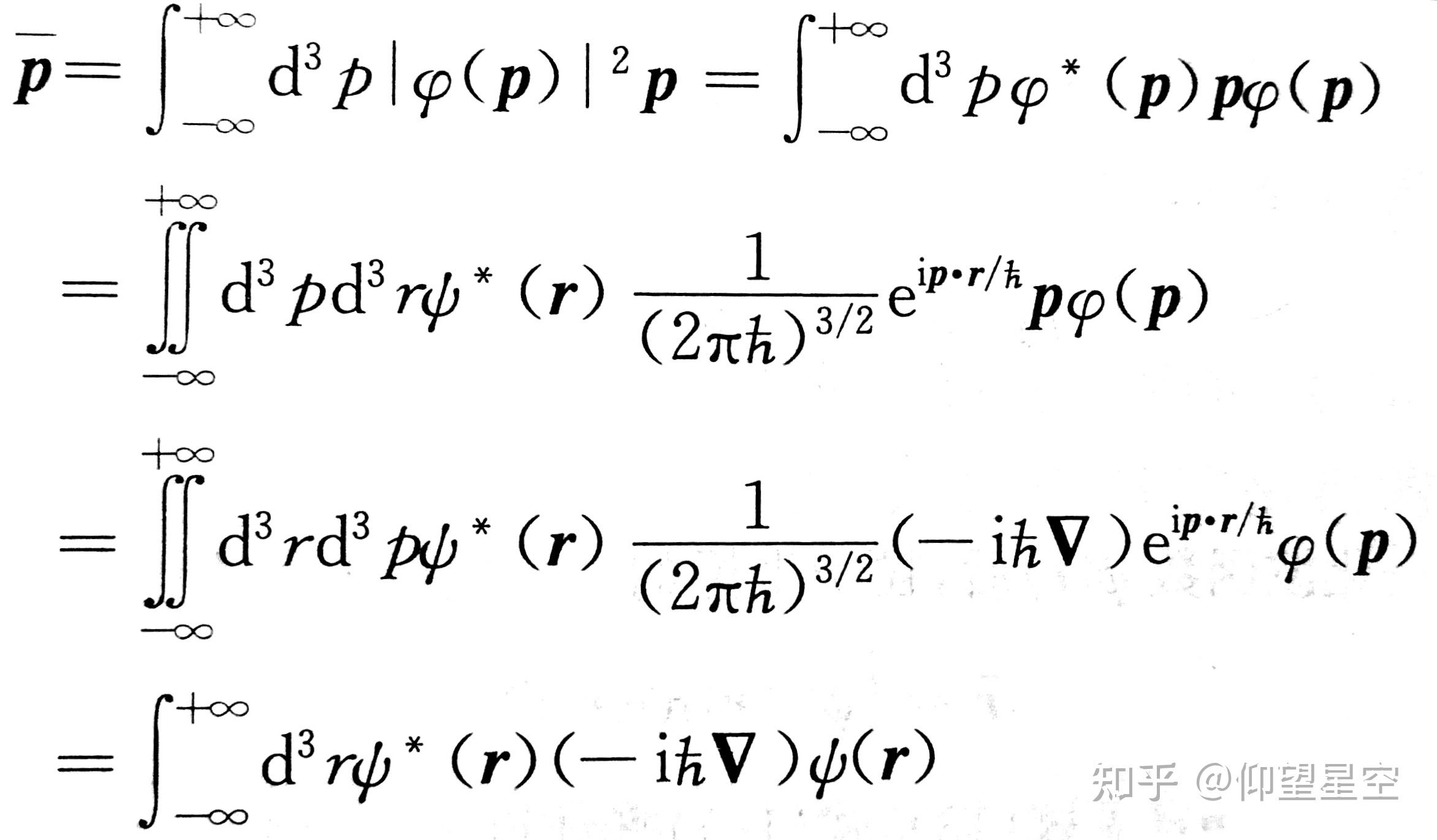


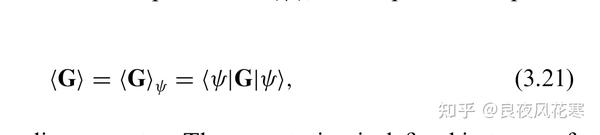
参考资料
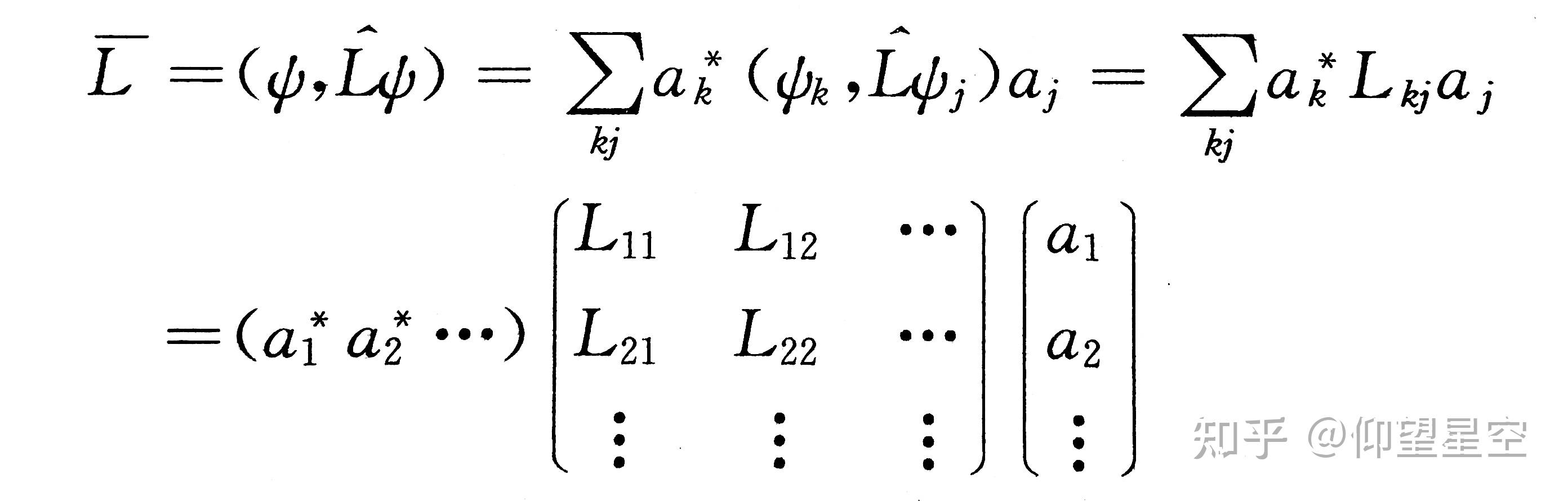
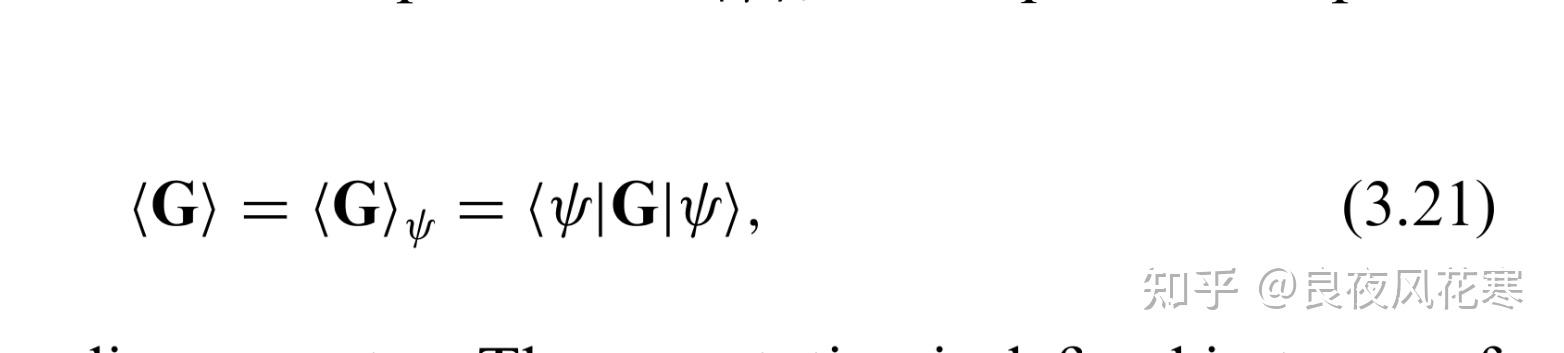
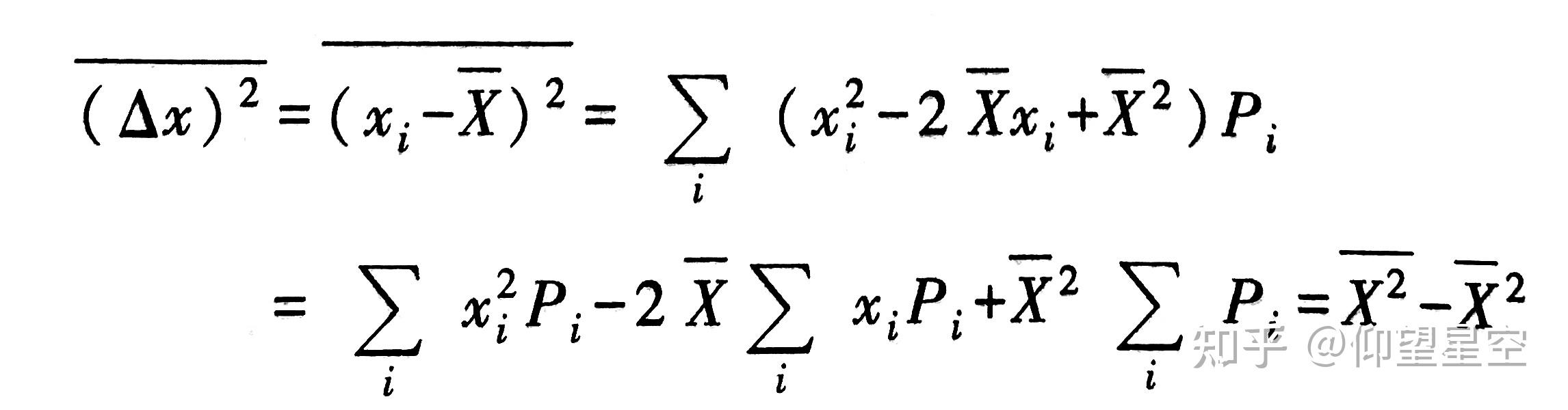
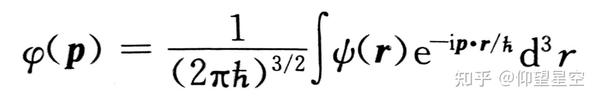
Moonshot回答
在量子力学中,可观测量的期望值是通过量子态的波函数(或密度矩阵)与对应可观测量的厄米算符相乘,然后取迹(trace)或积分来计算的。具体来说,如果 ( \hat{A} ) 是一个厄米算符,代表一个可观测量,( \psi ) 是系统的波函数,则该可观测量的期望值 ( \langle A \rangle ) 由下面的公式给出:
[ \langle A \rangle = \int \psi^* \hat{A} \psi , d\tau ]
其中 ( \psi^* ) 是波函数的复共轭,( d\tau ) 是体积元素。对于离散的波函数,积分将变为求和。
期望值在量子力学中代表的是大量重复实验中某物理量的统计平均值。由于量子力学本质上是概率性的,对单个量子系统进行测量可能得到不同的结果,但这些结果的统计平均将接近于期望值。例如,位置的期望值给出了粒子在空间中的平均位置,动量的期望值给出了粒子动量的平均大小。
从搜索结果中,我们可以看到一些相关的解释和公式。例如,维基百科上的解释指出,在量子力学中,重复做同样的实验通常会得到不同的测量结果,期望值是理论平均值,可以用来预测测量结果的统计平均值。此外,量子力学中的可观测量由厄米算符表示,它们的期望值是实数,这也是为什么它们在量子力学中如此重要的原因。
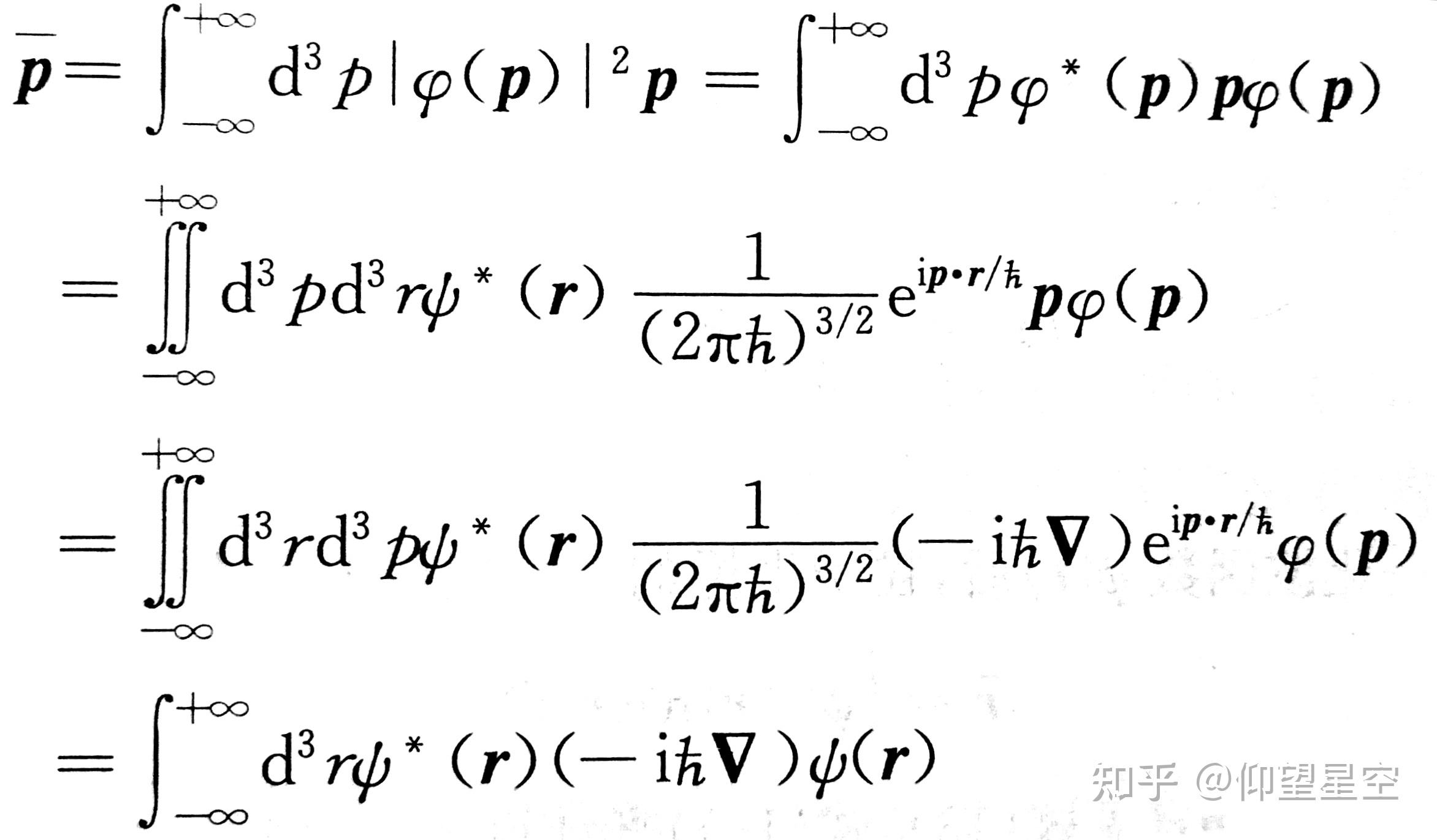
这张图片展示了量子力学中期望值的概念,其中包含了波函数和可观测量算符的表示。通过这些信息,我们可以更好地理解量子力学中期望值的计算和意义。