参考资料
参考资料




Moonshot回答
复杂系统在科学研究中有着广泛的应用,同时在研究过程中也面临着不少挑战。
典型应用:
-
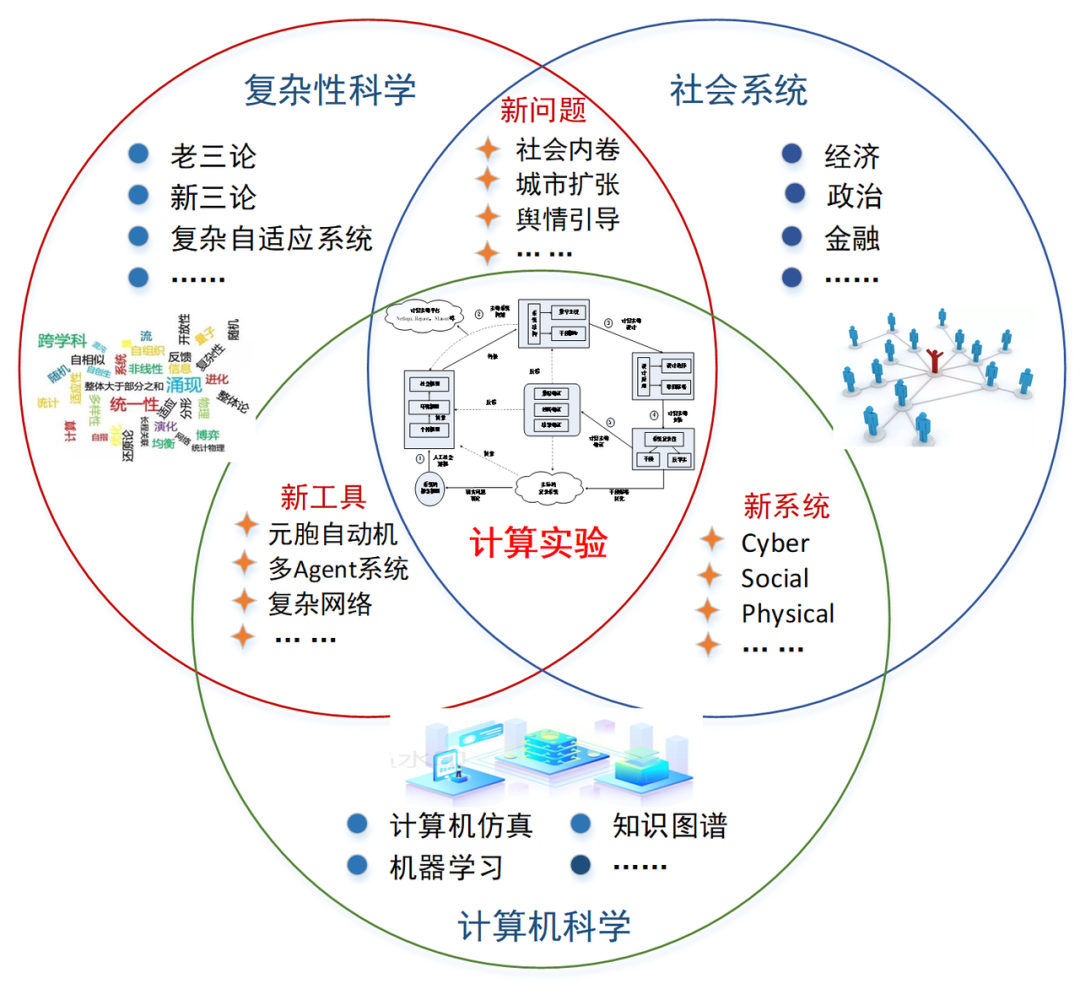
复杂系统科学原理介绍:复杂系统科学的目的是理解系统的一般属性,如复杂度曲线、有效性和适应性的权衡、系统复杂度与环境复杂度的匹配、多尺度分析和进化过程1。这些原理被应用于理解物理、生物和社会系统的复杂性。
-
经济社会系统:复杂系统理论被用于分析经济社会系统中的涌现行为,如市场竞争、创新和业务的发展1。
-
教育系统:教育系统在不同尺度上提供不同复杂度的教育方式,如大尺度低复杂度的电视教育和学校教育,以及小尺度高复杂度的一对一培训1。
-
组织管理:复杂系统理论被用于理解和优化组织结构,如公司通过合理的部门调整来应对不同业务需求1。
-
脑科学:复杂系统理论被应用于理解大脑的功能,探索神经网络结构与疾病和认知之间的关联[^3^]。
-
数字治理:复杂系统理论被用于数字治理领域,以改善政策制定和社会管理[^3^]。
-
军事科学:复杂系统理论也被应用于军事科学领域,以提高战略决策和系统效能[^3^]。
挑战:
-
跨学科研究:复杂系统研究通常需要跨学科合作,这要求研究人员具备多学科知识,并能整合不同领域的认识[^3^]。
-
数据建模:随着数据可获取性的提升,处理大规模异构数据并将其建模为动态系统是一个重要挑战[^3^]。
-
因果关系:超越相关关系,找到复杂系统中的因果关系是当前研究的焦点[^3^]。
-
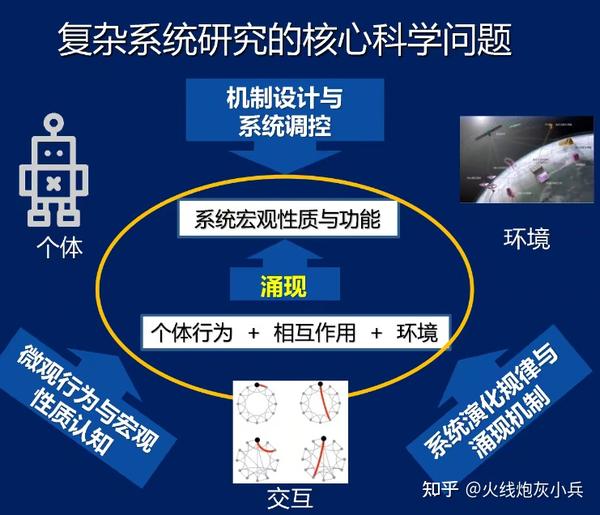
高阶相互作用:识别、量化和重构高阶相互作用,以及探索具有高阶相互作用的系统中复杂动力学涌现的基本原则是一个挑战[^3^]。
-
结合网络科学与人工智能:提出更好的理论和方法,以解决实际问题是复杂系统研究中的一个挑战[^3^]。
-
系统设计:设计系统以利用进化过程,使其能够适应不可预测性并随时间变得更加复杂1。
-
层次结构设计:设计合适的层次结构以促进有效的团队合作和竞争,这对于复杂系统的有效运作至关重要1。
综上所述,复杂系统科学在多个领域都有应用,但同时也面临着数据建模、跨学科研究、因果关系探索等方面的挑战。这些挑战需要科研人员进行更深入的研究和探索。

