参考资料

远地点（Apogee）和近地点（Perigee）是椭圆轨道上的两个特殊点。远地点是轨道上距离地球中心最远的点，而近地点则是距离地球中心最近的点。在轨道力学中，这些点对于轨道计算至关重要，因为它们影响轨道的形状和大小。

轨道的形状由偏心率（e）决定，偏心率可以通过远地点和近地点的距离计算得出。轨道的半长轴（a）是远地点和近地点距离的平均值，它决定了轨道的大小。轨道周期（T）是卫星绕地球一周所需的时间，它与半长轴的长度有关，具体关系由开普勒第三定律给出：[T = 2\pi \sqrt{\frac{a^3}{\mu}}]，其中(\mu)是地球的标准引力参数。

轨道设计时，需要考虑近地点和远地点的高度，以确保卫星能够到达预定的工作轨道。例如，地球同步转移轨道（GTO）的近地点高度约为200公里，远地点高度约为36000公里。通过霍曼转移轨道，卫星可以从低地球轨道（LEO）转移到GTO。

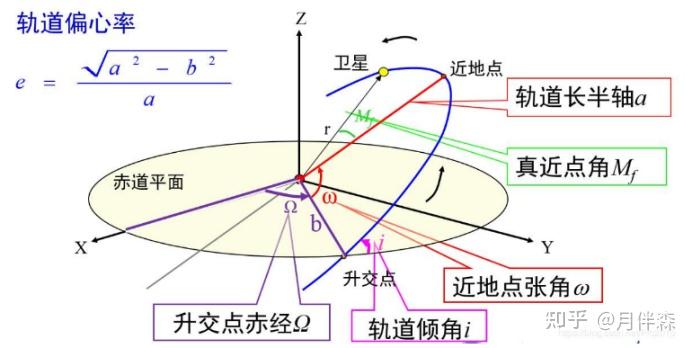
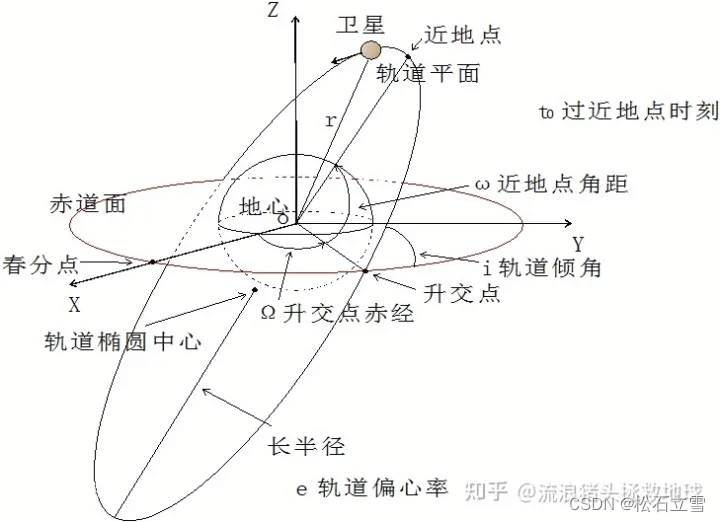
轨道计算时，除了远地点和近地点，还需要知道升交点赤经、近地点角距、经过近地点的时刻等参数。这些参数共同决定了卫星在轨道上的具体位置和运动状态。

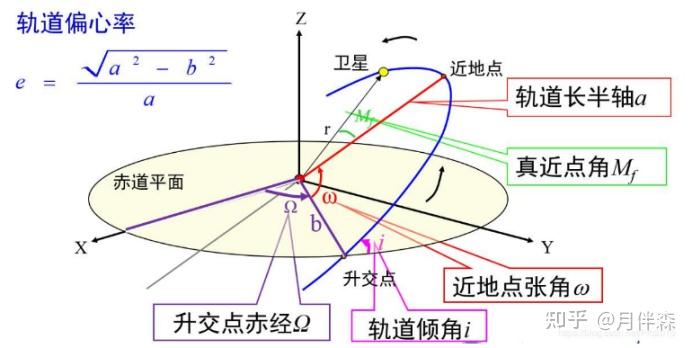
这张图展示了卫星在椭圆轨道上的远地点和近地点。通过这些信息，可以更准确地进行轨道计算和预测卫星的位置。