请解释扭曲几何中的“扭曲积度规”以及它的应用场景有哪些?
参考资料
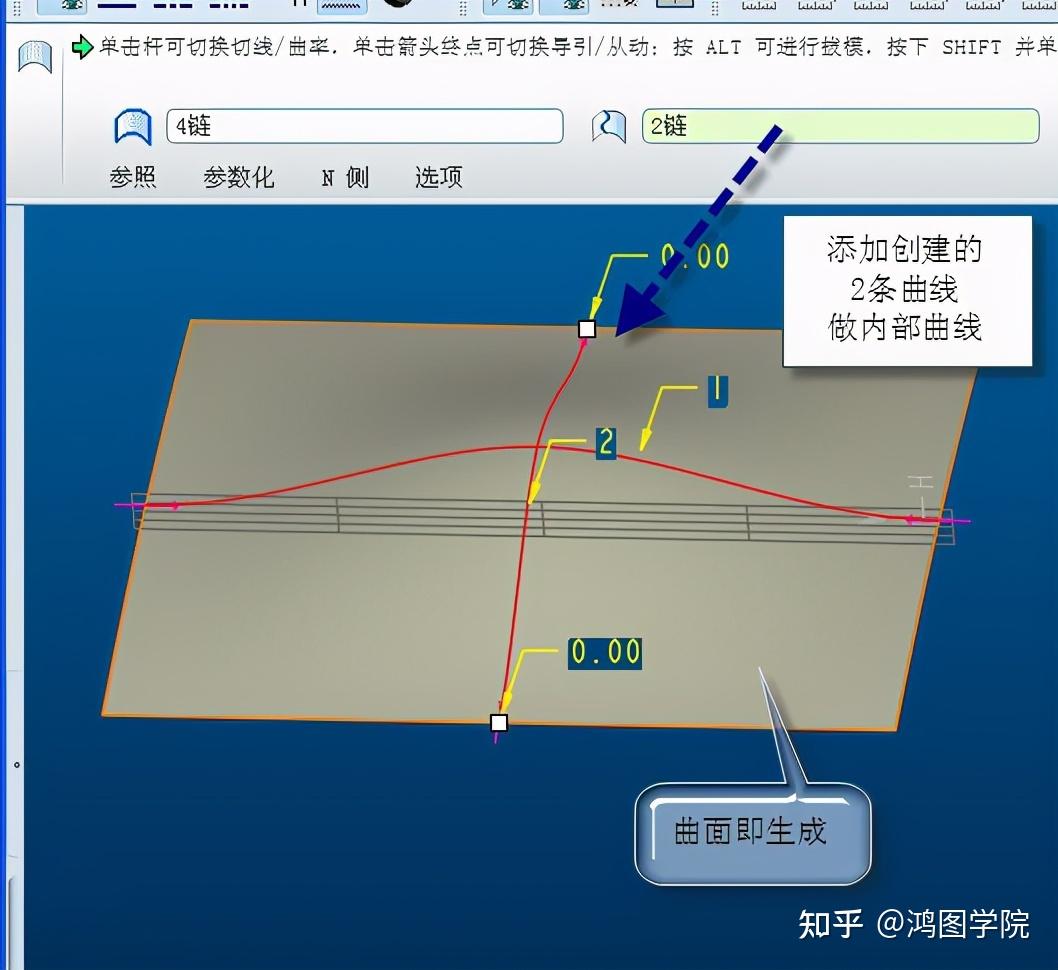
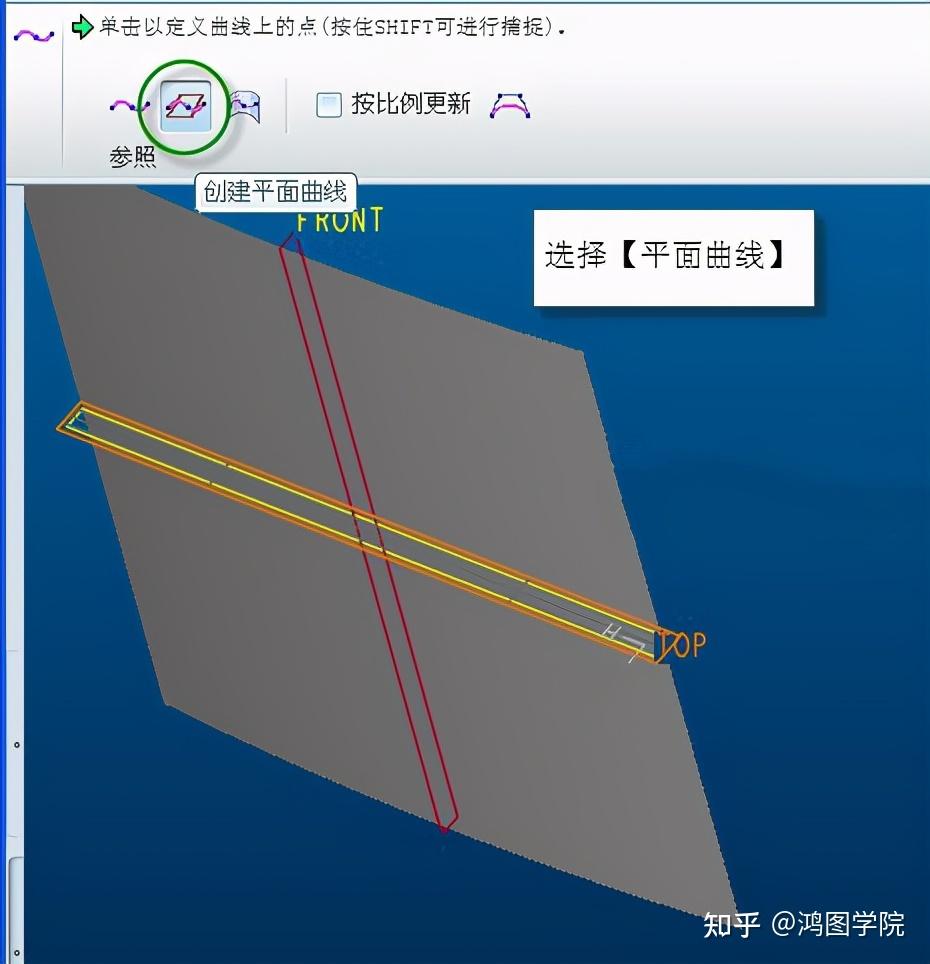
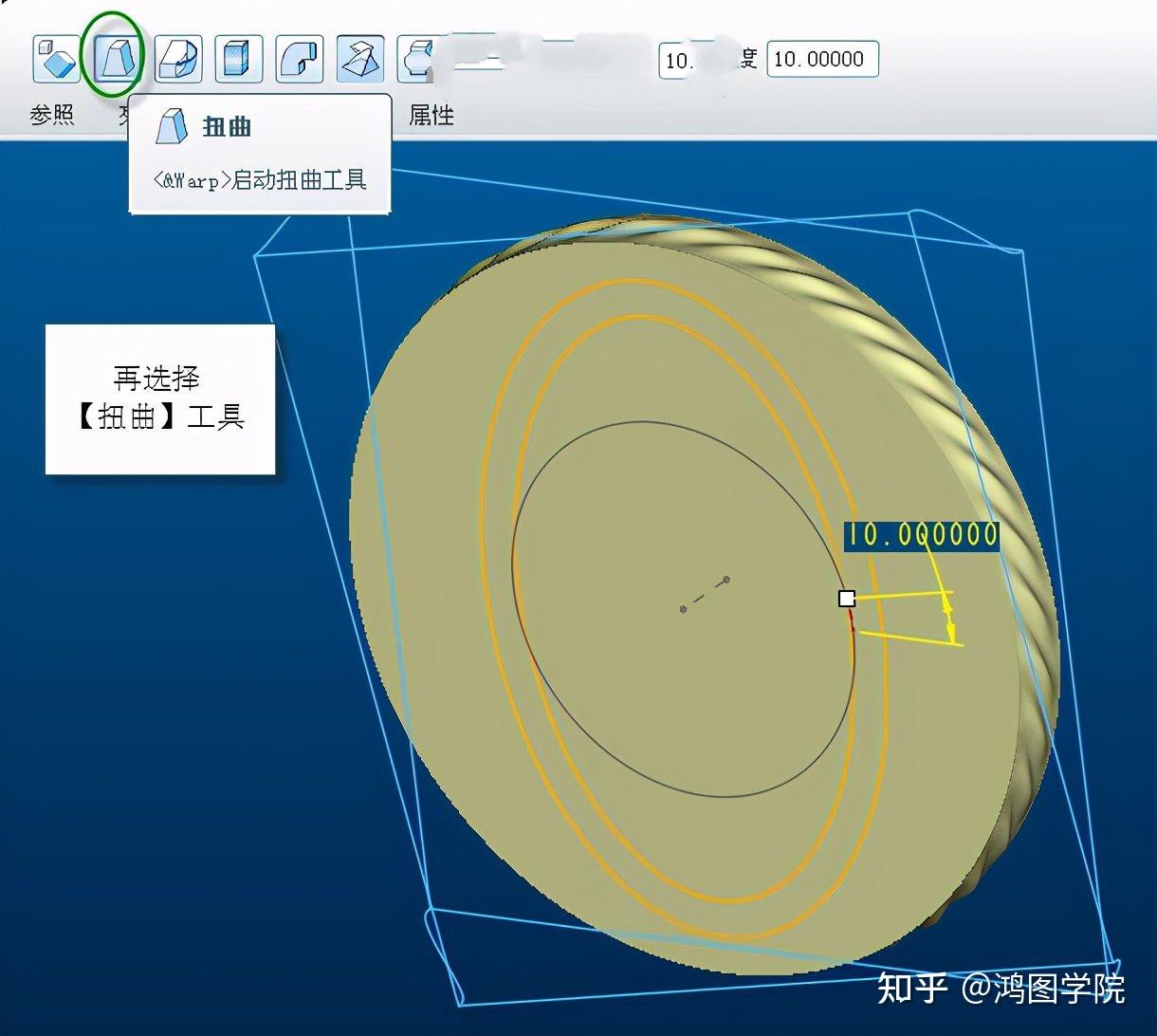
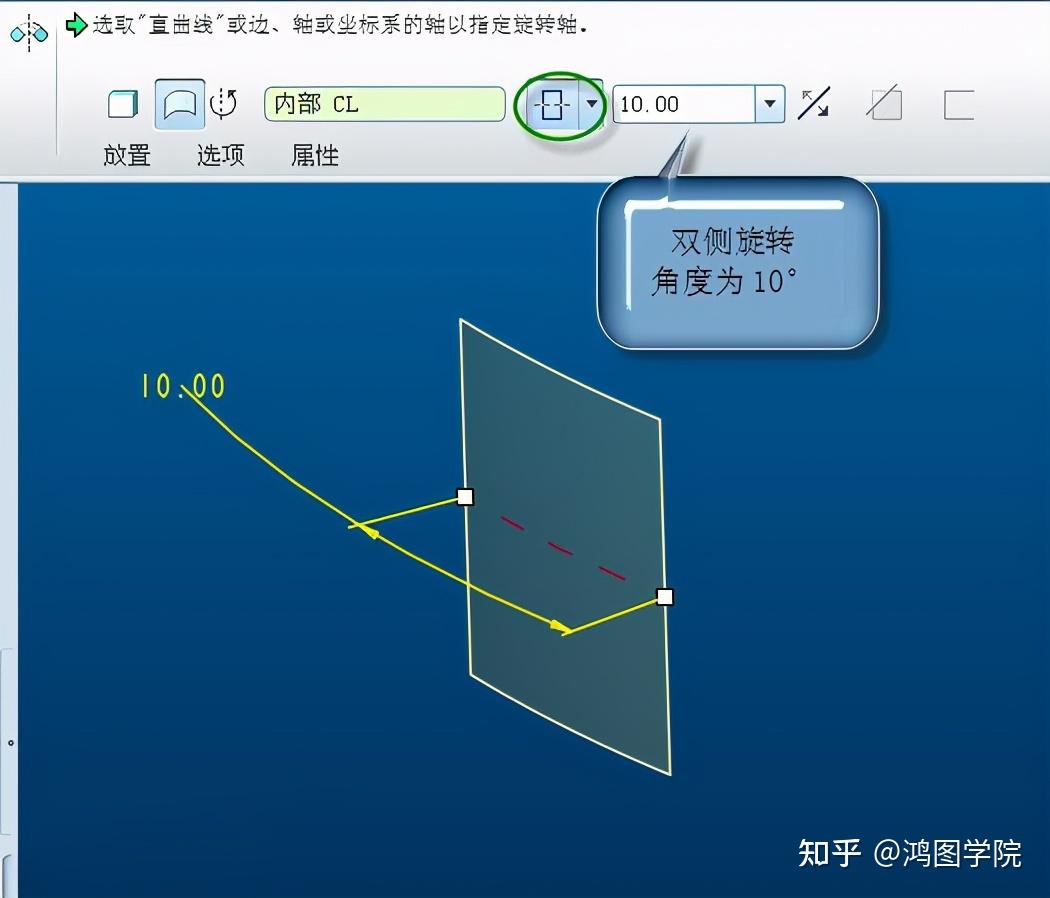
Moonshot回答
扭曲几何中的“扭曲积度规”(warped product metric)是一种特殊的度规张量,它描述了几何空间中的距离关系。这种度规张量可以写成两个子流形的卡氏积(Cartesian product)的形式,其中一个子流形的度量会根据另一个子流形的坐标受到扭曲。具体来说,如果一个几何空间可以分解为两个子空间的乘积,其中一个子空间的度量受到另一个子空间坐标的标量函数的调整,那么这个几何空间就具有扭曲积度规。
扭曲积度规在多个领域有着重要的应用,特别是在微分几何和广义相对论中。以下是一些主要的应用场景:
-
爱因斯坦场方程的解:许多爱因斯坦场方程的基本解是扭曲几何,例如史瓦西解和罗伯逊-沃尔克模型。这些解在描述宇宙的大尺度结构和黑洞的外部时空中起着关键作用。
-
分离变量法:扭曲几何允许使用分离变量法来解与其相关的偏微分方程,这在物理学和工程学中非常有用,尤其是在解决波动方程和热传导方程时。
-
自旋泡沫几何:在量子引力理论中,扭曲几何提供了一种理解自旋泡沫几何的新方法,这对于探索量子引力的微观结构具有重要意义。
-
结构工程:在结构工程中,扭曲几何可以用来分析具有初始曲线和扭曲形状的结构,如桥梁和建筑物,以及它们在不同载荷下的行为。
扭曲积度规因其在数学和物理学中的重要作用而受到广泛关注,它在解决复杂的几何和物理问题中提供了有力的工具。