参考资料

李雅普诺夫稳定性理论是由俄国数学家亚历山大·李雅普诺夫在1892年提出的，用于分析动态系统的稳定性。该理论主要关注系统在受到扰动后能否返回到其平衡状态。以下是李雅普诺夫稳定性理论的基本概念：

1. 平衡点：系统在没有外部影响时保持不变的状态。在数学上，这通常表示为系统导数为零的点。

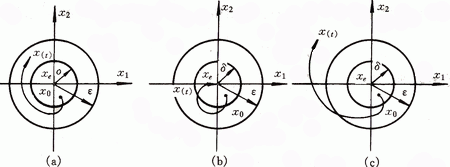
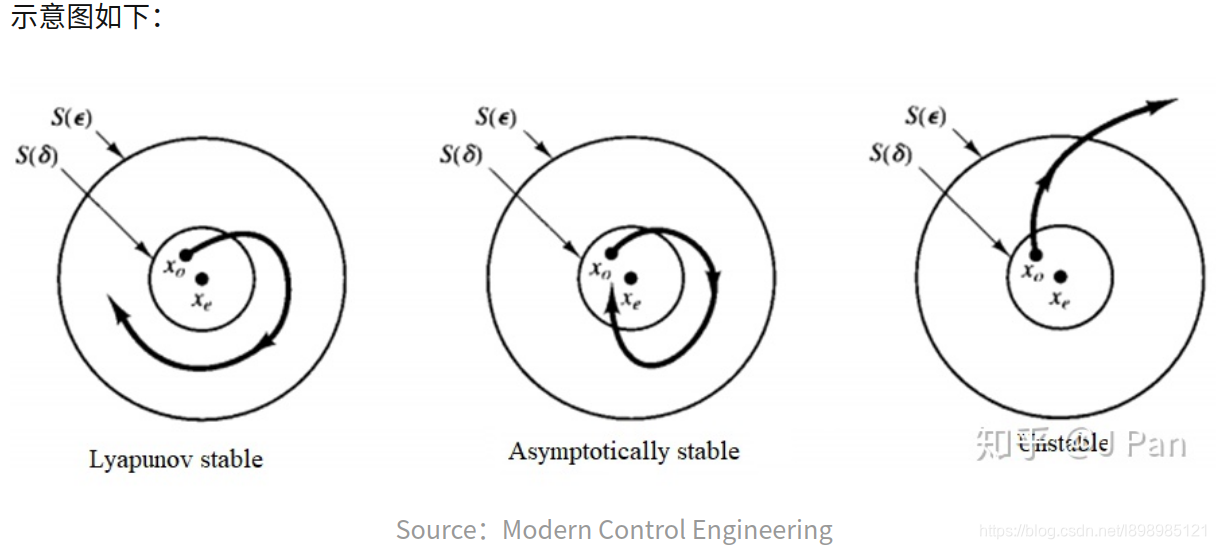
2. 稳定性：如果系统在受到小的扰动后能够返回到平衡点，那么这个平衡点被认为是稳定的。稳定性分为几种类型：

   • 李雅普诺夫稳定性：系统状态在受到扰动后能返回到平衡点附近，但不一定回到平衡点。
   • 渐近稳定性：系统状态不仅能够返回到平衡点附近，而且随着时间推移，能够无限接近或达到平衡点。
   • 不稳定平衡：系统在受到扰动后会远离平衡点。

3. 李雅普诺夫函数：一个标量函数V(x)，用于衡量系统状态与平衡点的距离。如果这个函数在平衡点附近是正定的，并且在系统演化过程中是负定的或负半定的，那么可以证明系统是稳定的。

4. 直接法和间接法：

   • 直接法：通过构造李雅普诺夫函数直接分析系统的稳定性，不需要求解微分方程。
   • 间接法：通过求解系统的微分方程，分析系统状态的演化来研究稳定性。

李雅普诺夫稳定性理论特别适用于非线性系统，因为它允许通过线性化方法来分析非线性系统的局部稳定性。这一理论在控制理论、力学、经济学等领域都有广泛的应用。

图片来源：网络搜索结果