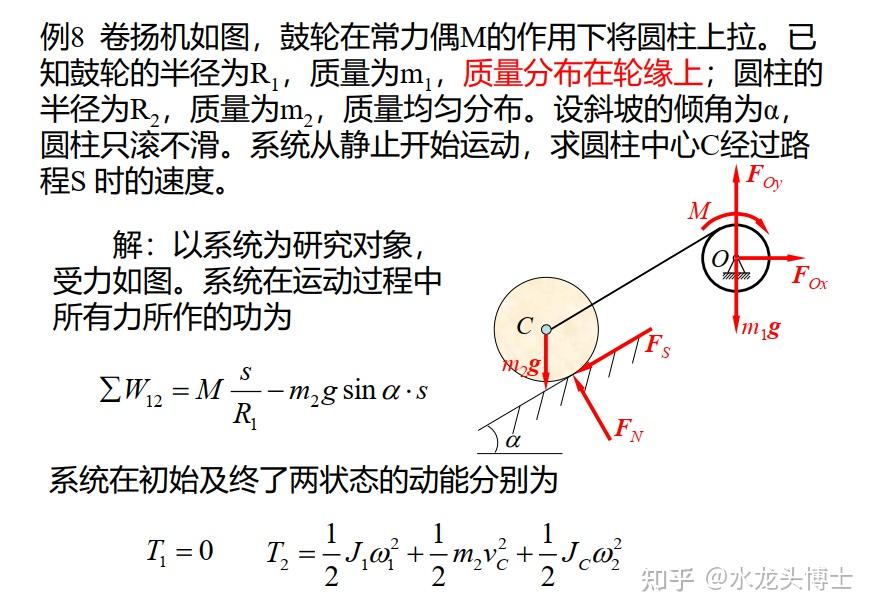
古典力学中的动能表达式和相对论中的动能表达式有什么区别?
参考资料




参考资料

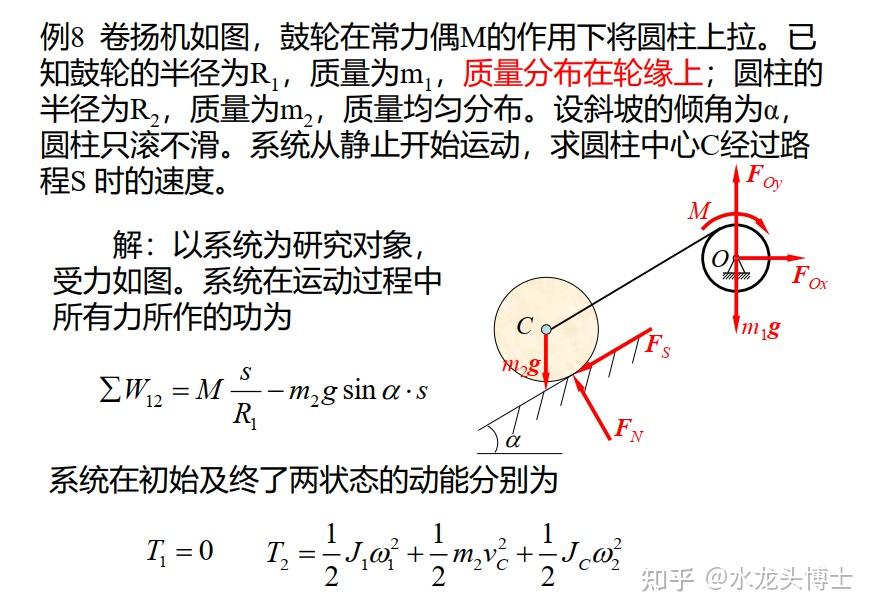
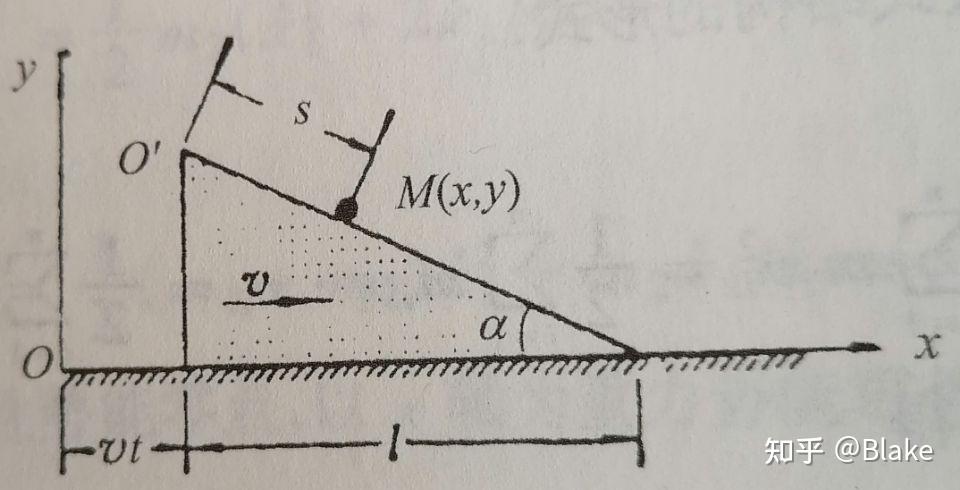

Moonshot回答
在古典力学中,动能的表达式是 ( E_k = \frac{1}{2}mv^2 ),其中 ( m ) 是物体的质量,( v ) 是物体的速度。这个表达式适用于宏观物体在低速运动时的情况,即速度远小于光速(( v \ll c ))。
而在相对论中,动能的表达式则更为复杂。相对论动能表达式为 ( E_k = mc^2 - m_0c^2 ),其中 ( m ) 是相对论质量,( m_0 ) 是静质量,( c ) 是光速。相对论质量 ( m ) 与速度 ( v ) 的关系为 ( m = \frac{m_0}{\sqrt{1 - \frac{v^2}{c^2}}} )。当速度远小于光速时,相对论动能表达式可以近似为古典力学的动能表达式。
相对论动能表达式与古典力学动能表达式的主要区别在于:
- 相对论考虑了质量随速度增加而增加的效应,而古典力学中质量是恒定不变的。
- 相对论动能表达式在速度接近光速时与古典力学动能表达式有显著差异,而在低速时两者近似相等。