正弦-戈尔登方程是什么?
参考资料


Moonshot回答
正弦-戈尔登方程是一种偏微分方程,首次在十九世纪被发现。方程表达式为: [ \varphi_{tt} - \varphi_{xx} = \sin(\varphi) ] 这个方程在数学和物理学中具有重要意义,特别是在研究孤立子现象时。它有一个几何解释,即三维欧几里德空间的负常曲率曲面(伪球面)。正弦-戈尔登方程与户田场论(Toda field theory)有关,并且在量子场论中,它是Thirring模型的S对偶。
正弦-戈尔登方程因其多种孤立子解而受到关注,这些孤立子解在不同的物理系统中有应用,例如在非线性光学、凝聚态物理和高能物理中。此外,正弦-戈尔登方程还与瞬子和孤子等概念相关。
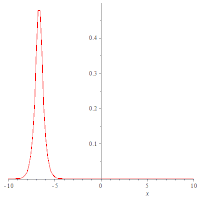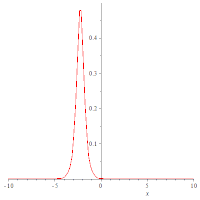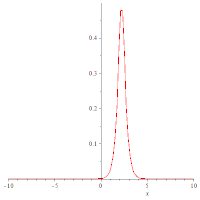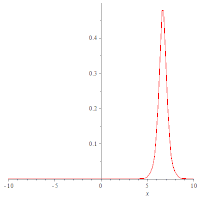
以下是一些正弦-戈尔登方程的动态图像,展示了其孤立子解的行为: