在海森堡绘景中,如何推导算符的时间演化方程?
参考资料

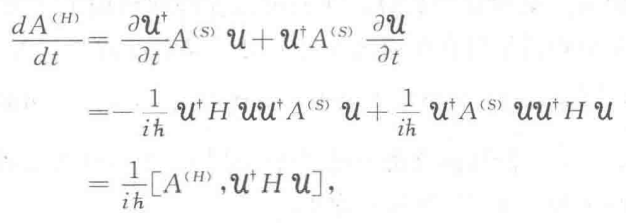


Moonshot回答
在海森堡绘景中,算符的时间演化方程可以通过以下步骤推导:
-
从薛定谔方程出发,该方程描述了量子态矢量随时间的演化。在薛定谔绘景中,态矢量随时间变化,而算符保持不变。
-
引入时间演化算符U(t, t0),它将时间t0的态矢量演化到时间t的态矢量,即ψ(t) = U(t, t0)ψ(t0)。
-
将时间演化算符应用于算符A,得到A_H(t) = U^\dagger(t, t0) A S(t, t0),其中A_H(t)是海森堡绘景中的算符,A是薛定谔绘景中的算符,U^\dagger是时间演化算符的厄米共轭。
-
利用薛定谔方程,对时间演化算符求导,得到iħ∂U/∂t = H(t)U,其中H(t)是系统的哈密顿量。
-
将U的表达式代入A_H(t)的表达式,并对A_H(t)关于时间求导,得到海森堡运动方程:iħ∂A_H/∂t = [A_H, H],其中[A_H, H]表示A_H和H的对易子。
-
海森堡运动方程描述了算符A_H随时间的演化,是海森堡绘景中的核心方程。
通过以上步骤,我们可以得到海森堡绘景中算符的时间演化方程。这一过程涉及到量子力学的基本概念,如态矢量、算符、薛定谔方程等。通过学习这些概念,我们可以更好地理解海森堡绘景及其在量子力学中的应用。来源