参考资料
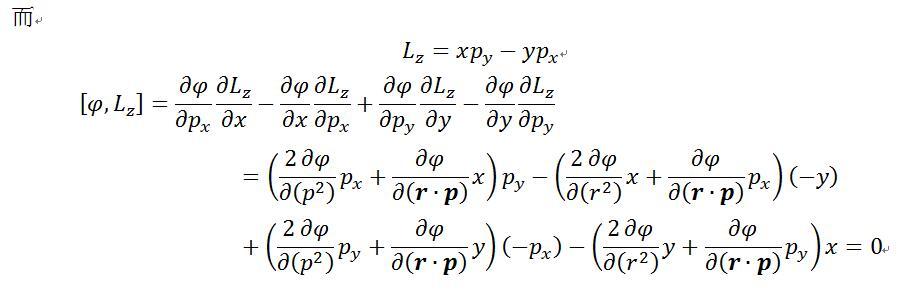

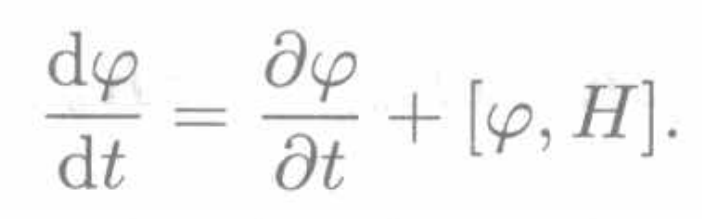
Moonshot回答
利用帕松括号描述角动量与LRL向量的保守性,我们可以从经典力学的角度出发。在经典力学中,角动量是一个重要的守恒量,其守恒性可以通过帕松括号与系统的对称性联系起来。根据Noether定理,物理系统的每一个连续对称性对应一个守恒定律。对于角动量守恒,这意味着如果系统的拉格朗日量在旋转变换下保持不变(即旋转对称),那么角动量就是守恒的。
帕松括号是哈密顿力学中描述物理量之间关系的数学工具。对于角动量向量 (\mathbf{L}) 和位置向量 (\mathbf{r}) 以及动量向量 (\mathbf{p}),它们的帕松括号定义如下: [ {L_i, r_j} = \epsilon_{ijk} r_k, \quad {L_i, p_j} = \epsilon_{ijk} p_k, ] 其中 (\epsilon_{ijk}) 是列维-奇维塔符号,表示完全反对称的符号函数。
在量子力学中,帕松括号被对易子所取代,但守恒的概念仍然适用。量子力学中的角动量算符 (\hat{L}_i) 满足类似的对易关系,并且如果系统的哈密顿量 (\hat{H}) 与旋转对称,则角动量算符与哈密顿量的对易子为零,表明角动量是守恒的。
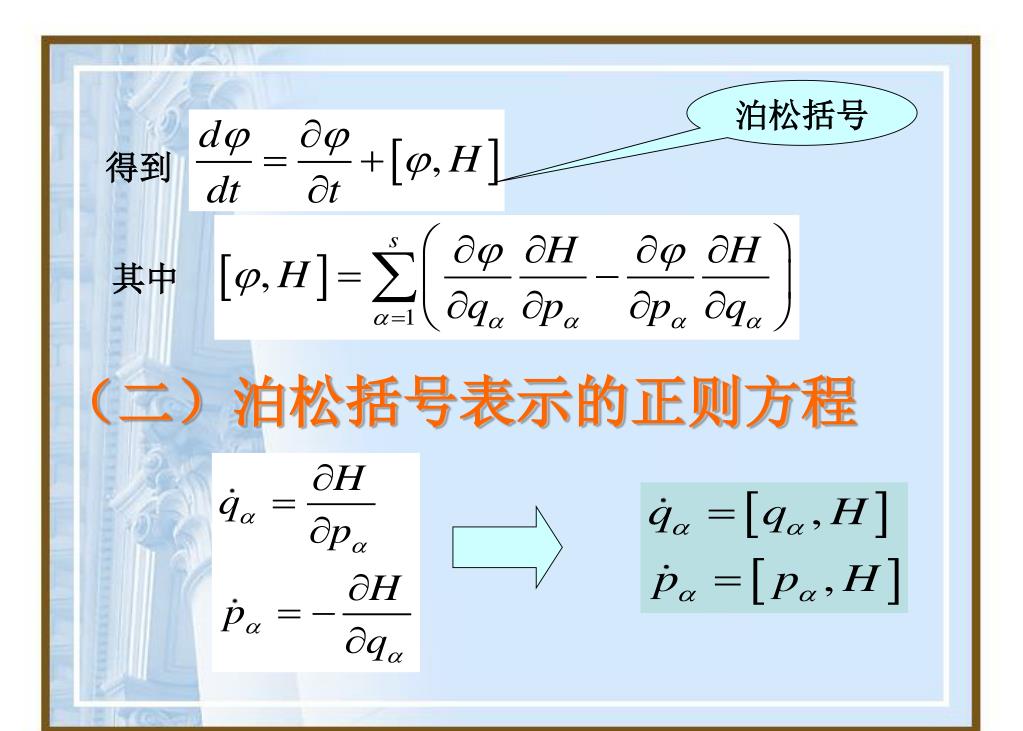
此外,LRL向量(位置、动量、角动量)的守恒性也可以通过帕松括号来描述。如果一个物理量 (A) 是守恒的,即 (\frac{dA}{dt} = 0),那么根据帕松括号的定义,(A) 与任何其他物理量 (B) 的帕松括号也将是守恒的。因此,如果角动量是守恒的,那么它与LRL向量的帕松括号也将是守恒的。
通过搜索结果,我们可以看到有关帕松括号与Noether定理的讨论,以及角动量守恒与系统对称性之间的关系。这些信息进一步支持了上述解释,并提供了更深入的理论背景。例如,文章《泊松括号与Noether定理》详细讨论了能量、动量和角动量守恒与相应对称性的关系。而《理论物理基础10:泊松括号,角动量和对称性》则提供了关于动量与角动量帕松括号的具体讨论。这些资源为我们提供了理解和描述角动量与LRL向量保守性的有力工具。