什么是拓扑矢量空间,它在数学和物理中的应用有哪些?
参考资料
参考资料



Moonshot回答
拓扑矢量空间(Topological Vector Space,简称TVS)是一个数学概念,它结合了拓扑空间和矢量空间的性质。具体来说,拓扑矢量空间是一个实数域或复数域上的矢量空间,同时也是一个拓扑空间,并且满足加法和数乘运算是连续的。这意味着,对于空间中的任意两个向量,它们的和以及与任何标量相乘的结果,仍然位于该空间内,并且这些操作在拓扑意义上是连续的。
拓扑矢量空间在数学和物理学中有广泛的应用。例如,在泛函分析中,拓扑矢量空间是研究连续线性算子和泛函分析的基本框架。在物理学中,它们被用于量子力学和量子场论中,以描述粒子的状态和演化。此外,拓扑矢量空间也在信号处理、图像分析和机器学习等领域中发挥作用,特别是在处理无穷维空间时。
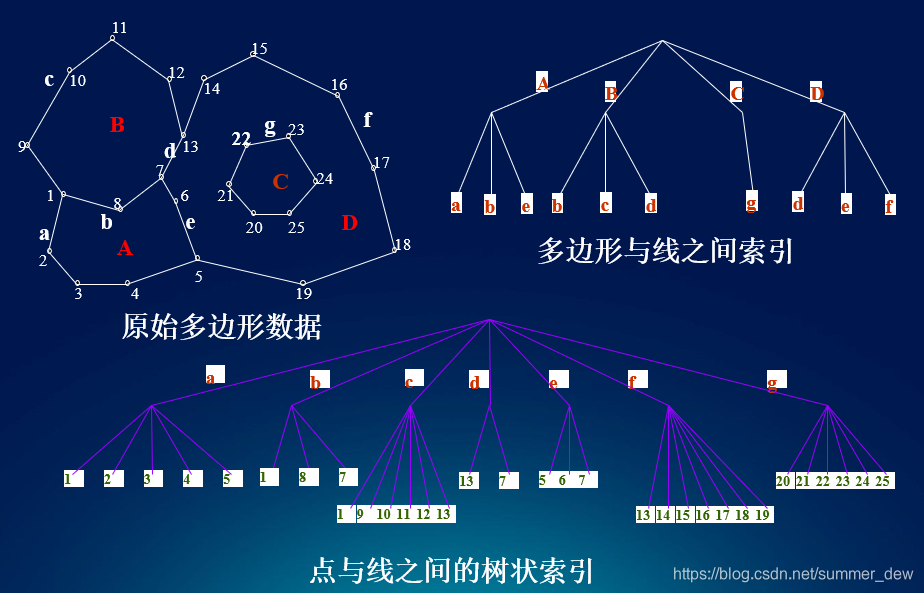
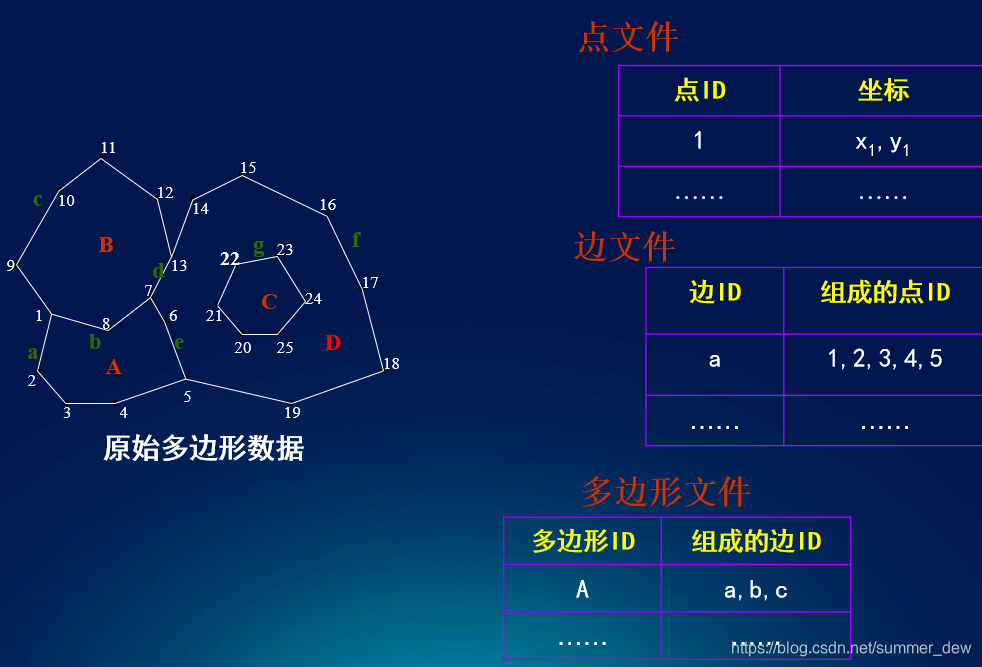
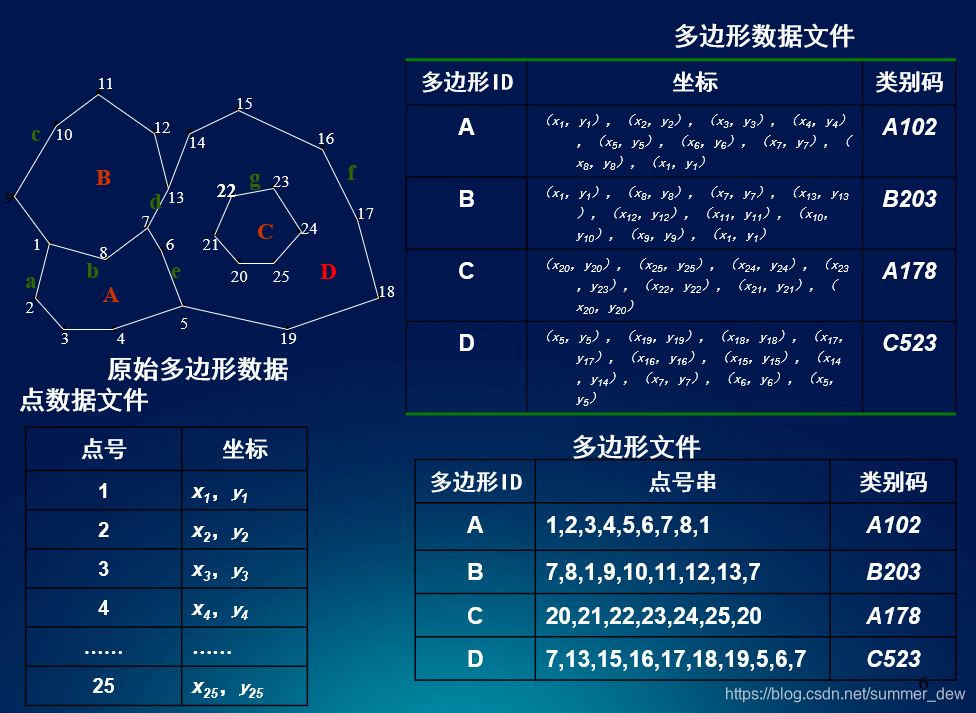
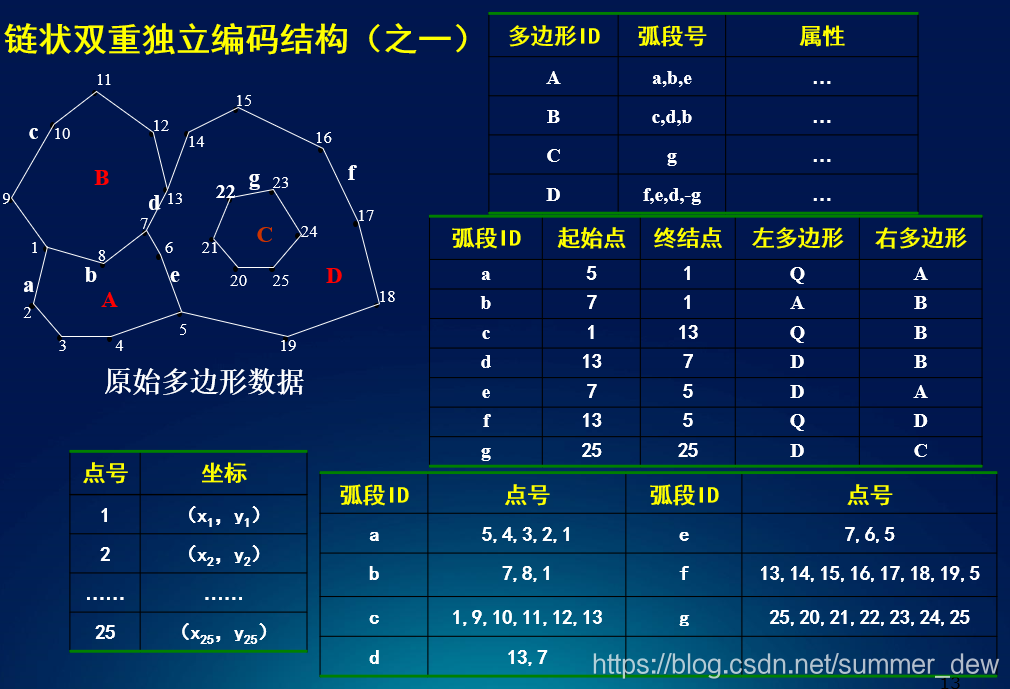
以下是一些与拓扑矢量空间相关的图像,可以帮助直观理解这一概念:


这些图像展示了拓扑矢量空间中的一些基本元素和结构,如开集、连续性和线性运算。通过这些图像,可以更直观地理解拓扑矢量空间的概念和性质。更多详细信息可以参考拓扑空间 - 维基百科和拓扑向量空间 - 小时百科。