使用萨赖法则和拉普拉斯展开法计算向量外积的过程是什么,以及它们的具体步骤分别是什么?
参考资料


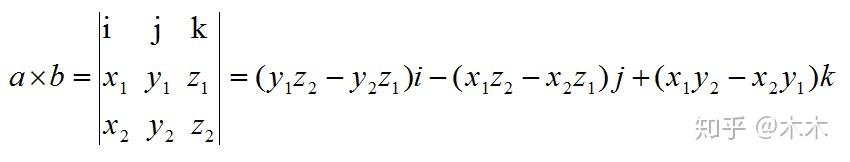

参考资料




Moonshot回答
萨赖法则和拉普拉斯展开法是两种不同的计算向量外积的方法。以下是它们的具体步骤:
-
萨赖法则:
- 首先定义向量外积:如果向量 (\mathbf{a}) 和 (\mathbf{b}) 的夹角为 (\theta),则外积定义为 (\mathbf{a} \times \mathbf{b} = |\mathbf{a}||\mathbf{b}|\sin(\theta)\mathbf{n}),其中 (\mathbf{n}) 是垂直于 (\mathbf{a}) 和 (\mathbf{b}) 的单位向量。
- 外积的绝对值表示两个向量张成的平行四边形的面积。
- 外积满足乘法分配律,即 (\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c})。
- 外积的反对称性:(\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a}))。
- 混合积性质:((\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c} = \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}))。
-
拉普拉斯展开法:
- 拉普拉斯展开通常用于计算行列式,但也可以用于向量外积的计算。
- 将向量外积表示为行列式的形式,例如在三维空间中,(\mathbf{a} \times \mathbf{b}) 可以表示为一个 3x3 行列式: [ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \end{vmatrix} ]
- 展开这个行列式,我们得到: [ \mathbf{a} \times \mathbf{b} = (a_2b_3 - a_3b_2)\mathbf{i} - (a_1b_3 - a_3b_1)\mathbf{j} + (a_1b_2 - a_2b_1)\mathbf{k} ]
- 这个公式给出了向量 (\mathbf{a}) 和 (\mathbf{b}) 外积的坐标形式。
这两种方法都可以用于计算向量外积,选择哪一种取决于具体问题和个人偏好。萨赖法则更侧重于向量的几何意义,而拉普拉斯展开法则提供了一种代数上的计算方式。来源:知乎 和 维基百科。