动量守恒如何通过纳维-斯托克斯方程描述地球表面流体的动力学?
参考资料


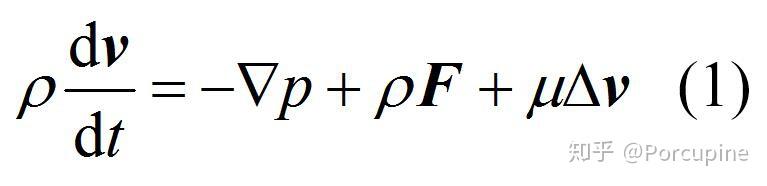
Moonshot回答
动量守恒在流体动力学中通过纳维-斯托克斯方程(Navier-Stokes equations)来描述。纳维-斯托克斯方程是一组描述粘性流体运动的非线性偏微分方程,它们基于动量守恒原理,考虑了流体的粘性效应。这些方程可以表示为:
[ \rho \left( \frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} \right) = -\nabla p + \mu \nabla^2 \mathbf{u} + \mathbf{f} ]
其中,(\rho) 是流体密度,(\mathbf{u}) 是流体速度矢量,(p) 是压力,(\mu) 是动力粘性系数,(\mathbf{f}) 是单位质量的外力。
在地球表面流体动力学中,纳维-斯托克斯方程能够描述大气和海洋等流体的运动。例如,它们可以用于模拟风和洋流的形成,以及它们如何受到地球自转和地形的影响。这些方程在天气预报、气候变化研究和海洋学等领域有着广泛的应用。

由于纳维-斯托克斯方程的复杂性,直接求解这些方程通常非常困难,尤其是在三维情况下。因此,科学家和工程师经常使用计算流体动力学(CFD)软件来数值求解这些方程,以模拟和分析流体流动。
总的来说,动量守恒原理通过纳维-斯托克斯方程在地球表面流体动力学中得到了详细的描述和应用。这些方程不仅帮助我们理解流体运动的基本规律,还为解决实际问题提供了强大的工具。