什么是牛顿法,以及它在什么情况下适用?
参考资料

参考资料



Moonshot回答
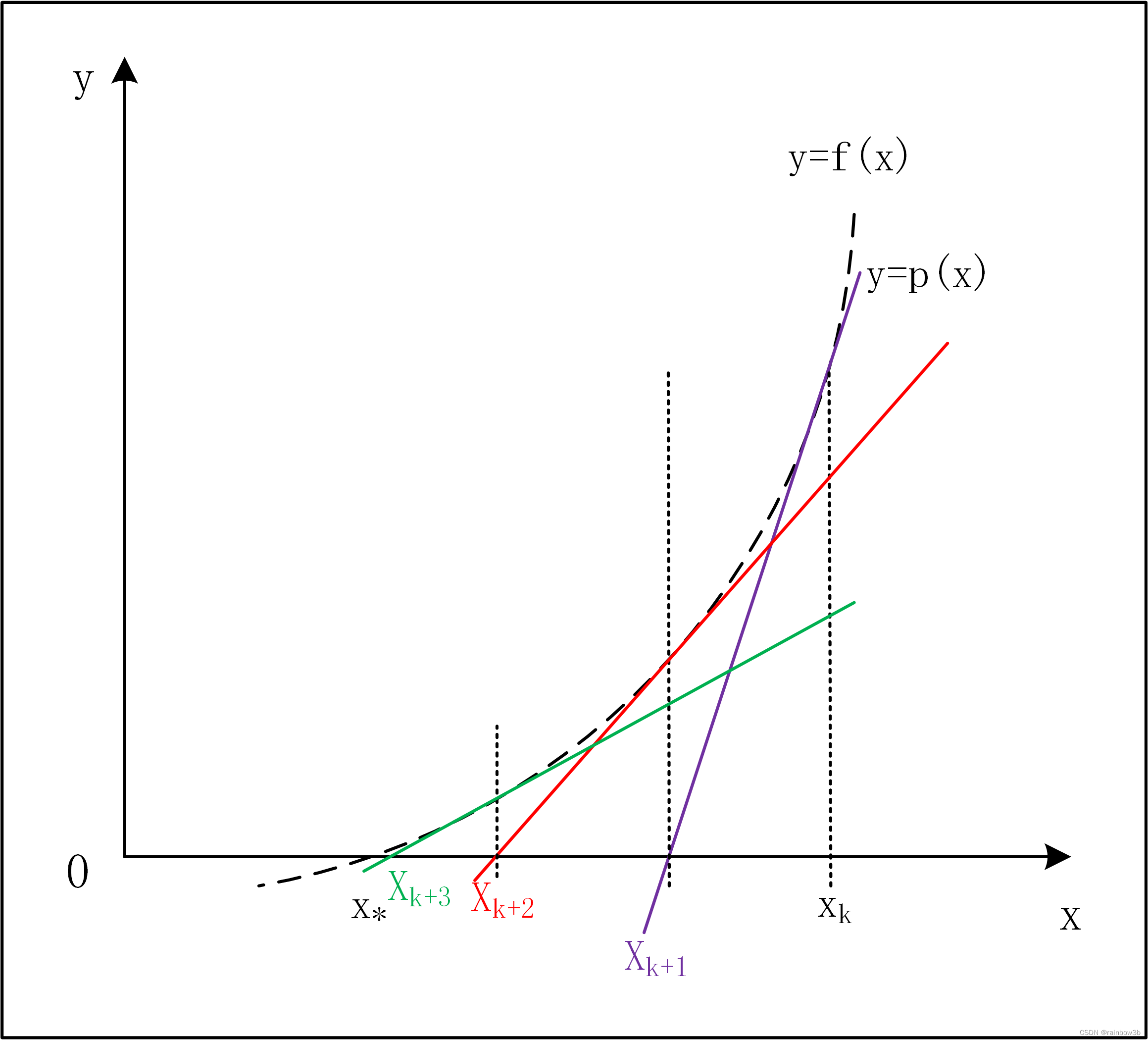
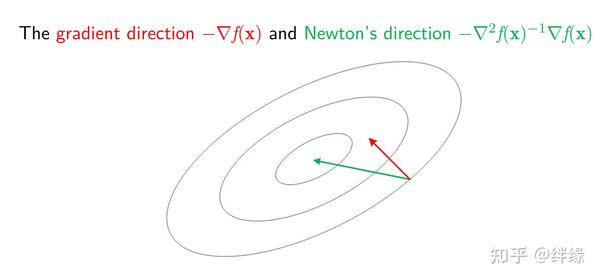
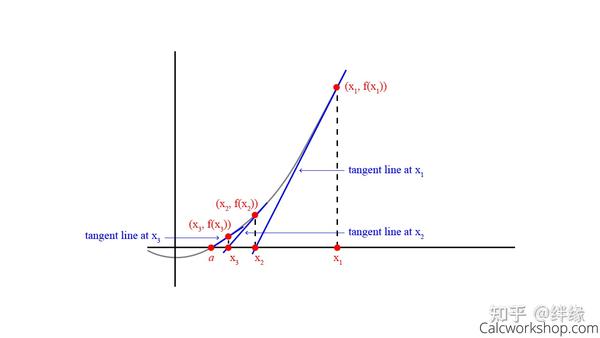
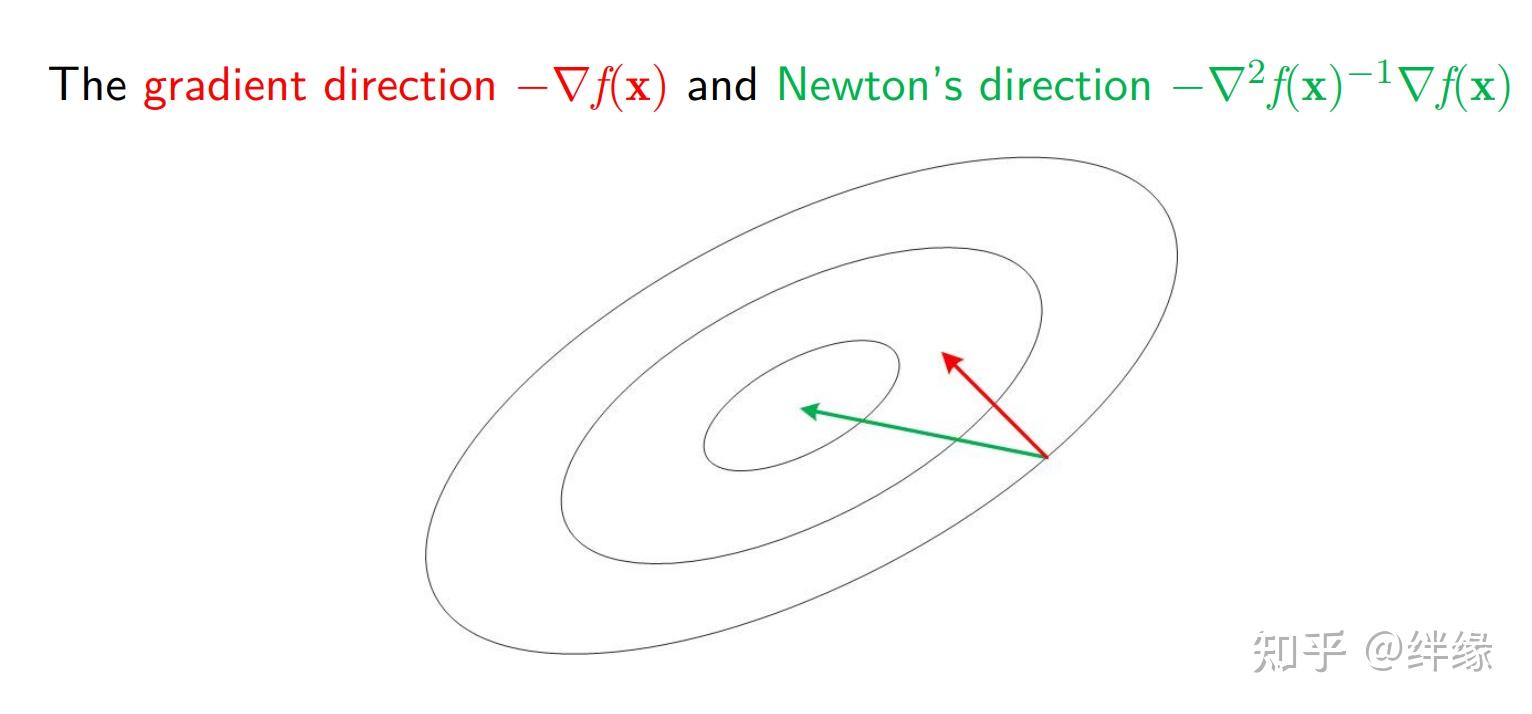
牛顿法(Newton's method),也称为牛顿-拉弗森方法(Newton-Raphson method),是一种用于在实数域和复数域上近似求解方程的方法。它基于函数的泰勒级数展开,通过迭代逼近函数的根或极小值点,以寻找函数的最优解。牛顿法使用函数的一阶导数(梯度)和二阶导数(Hessian矩阵)来寻找极值点,因此它是一种二阶优化算法。
牛顿法的迭代公式为: [ x_{n+1} = x_n - \frac{f'(x_n)}{f''(x_n)} ] 其中,( x_n ) 是当前迭代点,( f'(x_n) ) 是函数在 ( x_n ) 处的一阶导数,( f''(x_n) ) 是函数在 ( x_n ) 处的二阶导数。
牛顿法在以下情况下适用:
- 目标函数是二阶连续可微的。
- 函数的Hessian矩阵(二阶导数矩阵)是正定的,以确保算法的收敛性。
- 当需要解决最小二乘问题时,高斯-牛顿法是一个适合的选择。
- 在机器学习领域,牛顿法适用于高维优化和特定模型训练,尤其是当数据量不是非常大时。
然而,牛顿法也有局限性,例如:
- 对于大规模问题,计算和存储Hessian矩阵的成本很高。
- 牛顿法是局部收敛的,这意味着如果初始猜测不够接近真实根,算法可能不会收敛到正确的解。

图片来源:知乎专栏
在实际应用中,根据问题的特性和规模,可能会选择牛顿法的变种,如拟牛顿法,以减少计算复杂度。例如,L-BFGS算法适合处理大规模优化问题,因为它不需要存储完整的Hessian矩阵。梯度下降法、牛顿法、拟牛顿法 三类迭代法应用场景有何差别?