准正态模式的数学表达式是什么样子的?
参考资料



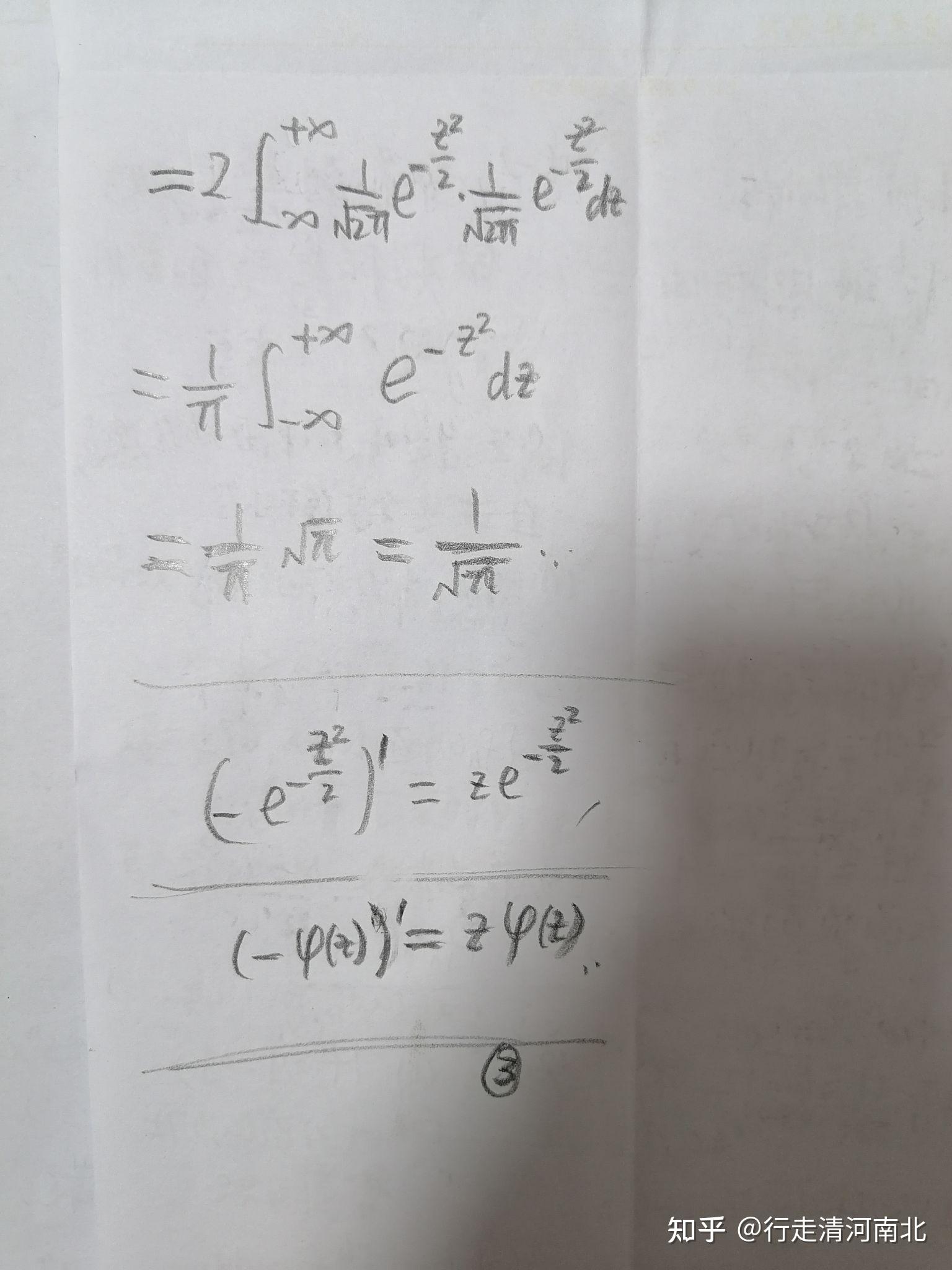
Moonshot回答
准正态模式的数学表达式通常指的是正态分布的概率密度函数(PDF)。正态分布的概率密度函数的一般形式是:
[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} ]
其中:
- ( \mu ) 是分布的均值(期望值)。
- ( \sigma ) 是分布的标准差。
- ( e ) 是自然对数的底数,约等于2.71828。
- ( \pi ) 是圆周率,约等于3.14159。
正态分布的概率密度函数图像是一个对称的钟形曲线,均值 ( \mu ) 决定了曲线的中心位置,而标准差 ( \sigma ) 决定了曲线的宽度。标准正态分布是均值为0,标准差为1的正态分布,其概率密度函数为:
[ f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} ]

这个图像展示了正态分布曲线的形状,其中心位于均值 ( \mu ),并且随着距离均值的增加,曲线的高度逐渐减小。