参考资料

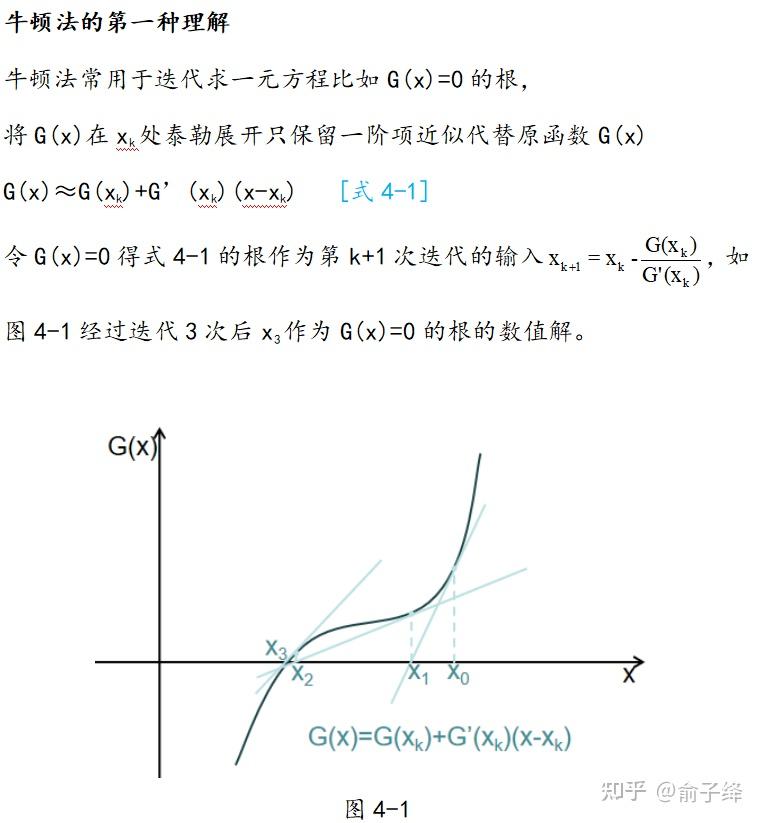
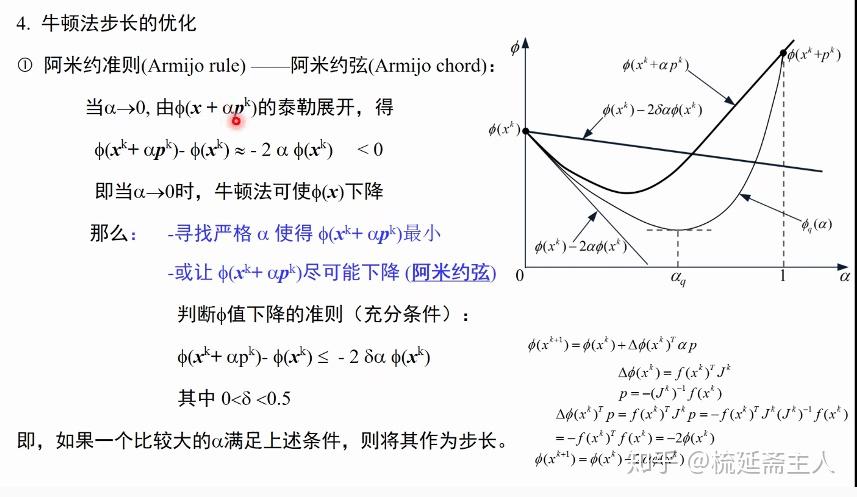
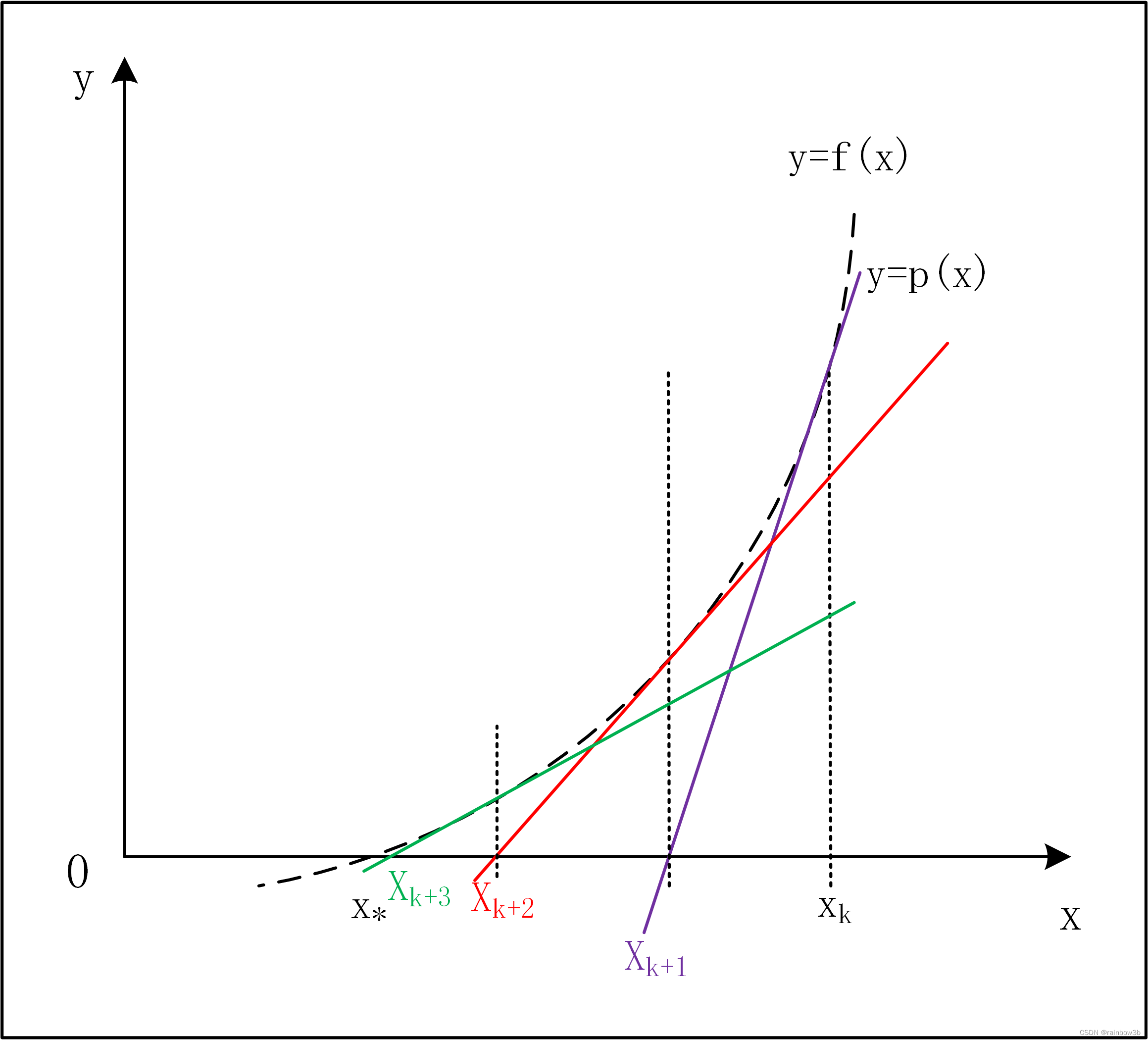
牛顿法是一种求解优化问题的方法，它通过二阶函数逼近来寻找函数的极小值点。具体来说，牛顿法的基本思想是在极小点附近用二阶泰勒多项式近似目标函数f(x)，进而求出极小点的估计值。这种方法利用了迭代点的梯度信息和二阶导数对目标函数进行二次函数逼近，然后把二次函数的极小值作为新的迭代点，并不断重复这一过程。

牛顿法的核心步骤包括选择一个初始点x0，然后在每一步迭代中计算函数f(x)在当前点x的梯度（一阶导数）和黑塞矩阵（二阶导数）。通过这些信息，可以构建一个二次模型来逼近原函数，并找到这个二次模型的极小值点，以此作为新的迭代点。

除了基本的牛顿法，还有拟牛顿法，如BFGS和DFP方法，它们在不需要计算二阶导数的情况下近似牛顿法的效果。高斯-牛顿法是另一种变体，它适用于求解最小二乘问题，通过最小化误差的平方和来寻找参数的最优解。

这些方法在机器学习、优化问题等领域有广泛的应用。例如，在这篇文章中，作者详细介绍了如何用Python实现牛顿法来求解最小值问题，包括拟牛顿法的实现。而在知乎的这篇文章中，作者解释了牛顿法的基本思想，并讨论了其在数值优化中的应用。