杜哈梅积分在振动理论中的主要用途是什么？
参考资料
Moonshot回答
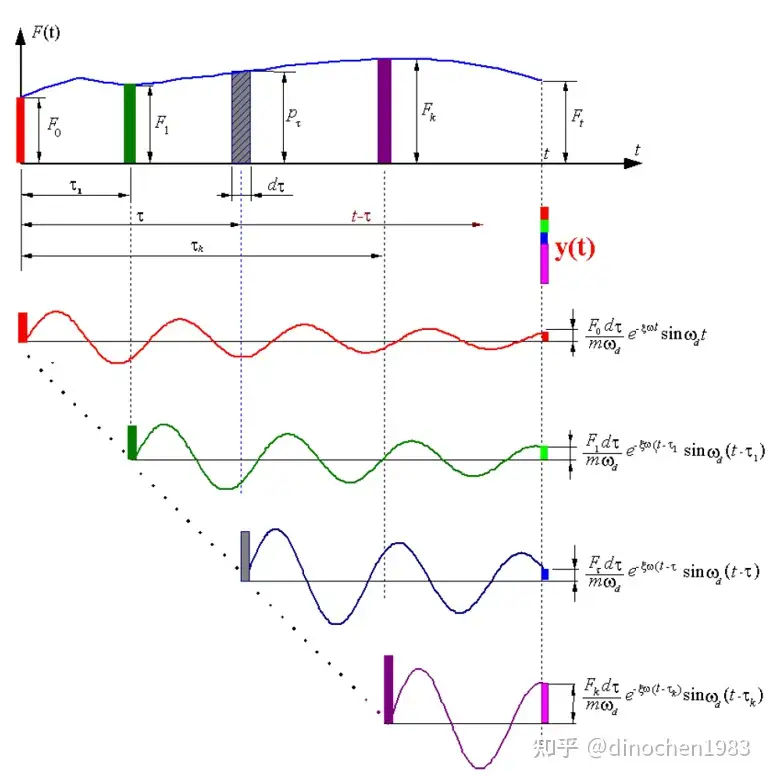
杜哈梅积分在振动理论中的主要用途是求解线性系统在任意外载激励下的响应。具体来说，它通过将外激励分解成无穷多个微冲量作用，然后对求得的各微冲量响应进行积分叠加来求解。这种方法特别适用于单自由度线性振动系统，并且可以处理零初值条件下的系统响应。杜哈梅积分是脉冲响应函数与激励函数的卷积积分，其数学表达式为：
[ x(t) = \int_0^t h(t-\tau) F(\tau) d\tau ]
其中，( h(t) ) 是系统的脉冲响应函数，( F(t) ) 是外载激励函数。
此外，杜哈梅积分在处理受随时间变化的外载和粘性阻尼作用下的线性单自由度系统的二阶常微分方程时也非常有用。它不仅在理论上有重要意义，而且在工程实践中也具有广泛的应用价值，例如在结构动力学、机械振动等领域。
继续提问
相关问题
不同类型的多参考组态相互作用方法如MRCIS和MRCISD分别有什么特点？
Unearthed Films发行的电影中，包含哪些剥削电影或与剥削电影相关的片名？
电影《田纳西》中有哪些主要演员？
什么是历元J2000.0，相对于其它历元它有何特别之处？
开尔文探针力显微鏡除了可以检测原子之间的作用力，还有哪些其他具体的应用？
中苏关系在苏共二十二大之后为何迅速恶化，并最终导致中苏决裂？
格拉德和沙夫拉诺夫在等离子体物理研究方面有哪些贡献？
简·考尔是在哪一年出生的，出生时的名字是什么？
为什么当前我国经济增长压力较为突出，尤其是需求端出现了明显的低迷情况？
《流星语》中的狄龙和吴家丽分别获得了哪些电影奖项的认可？