Ising模型中的传递矩阵是如何构建的,其物理意义是什么?
参考资料


参考资料



Moonshot回答
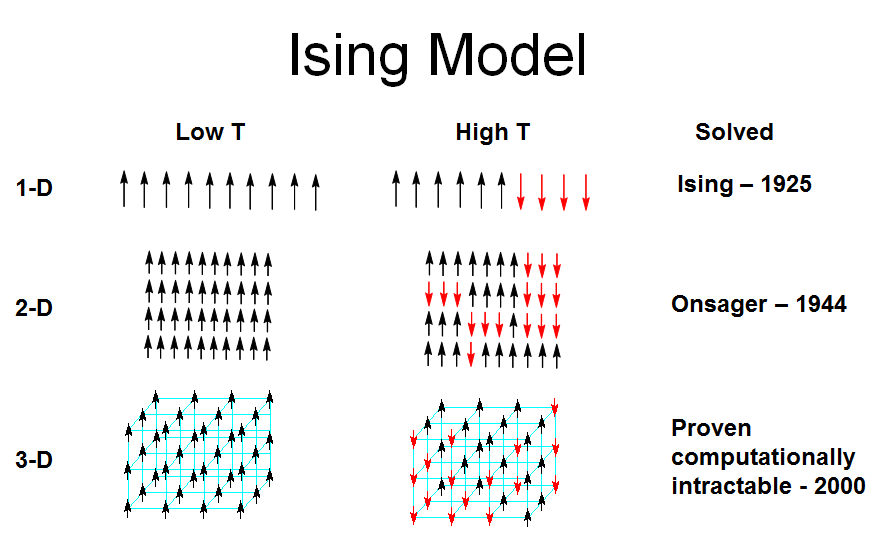
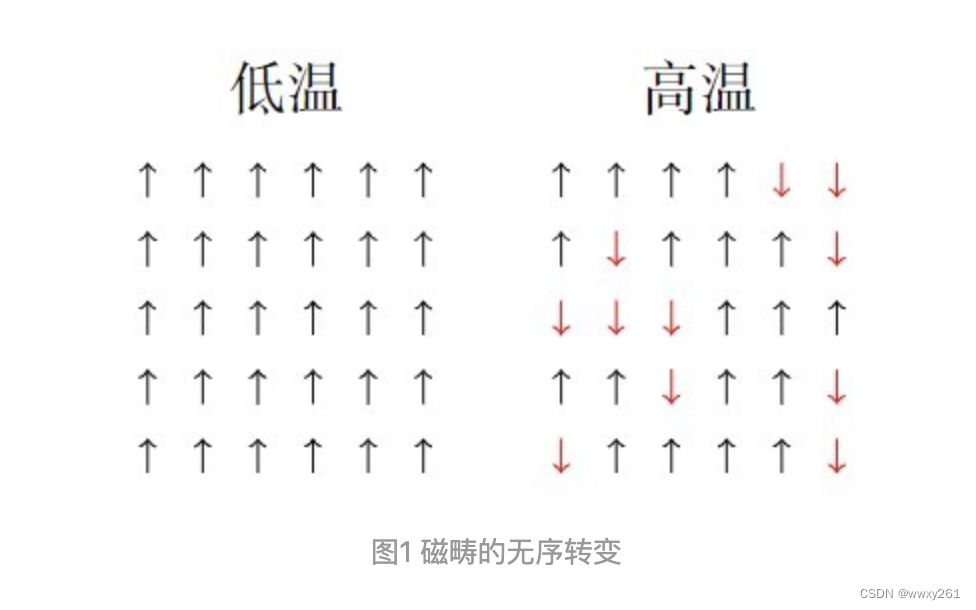
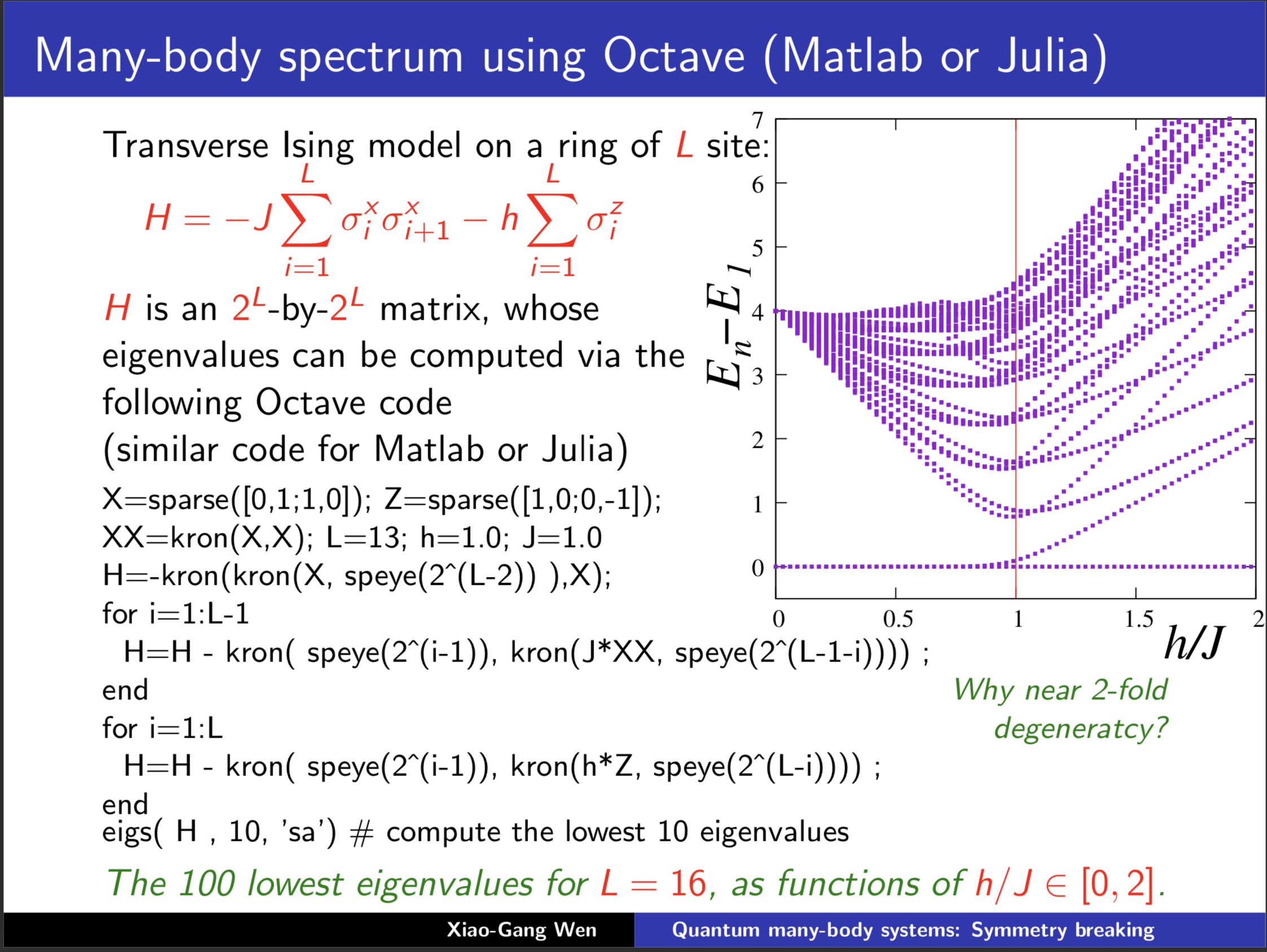
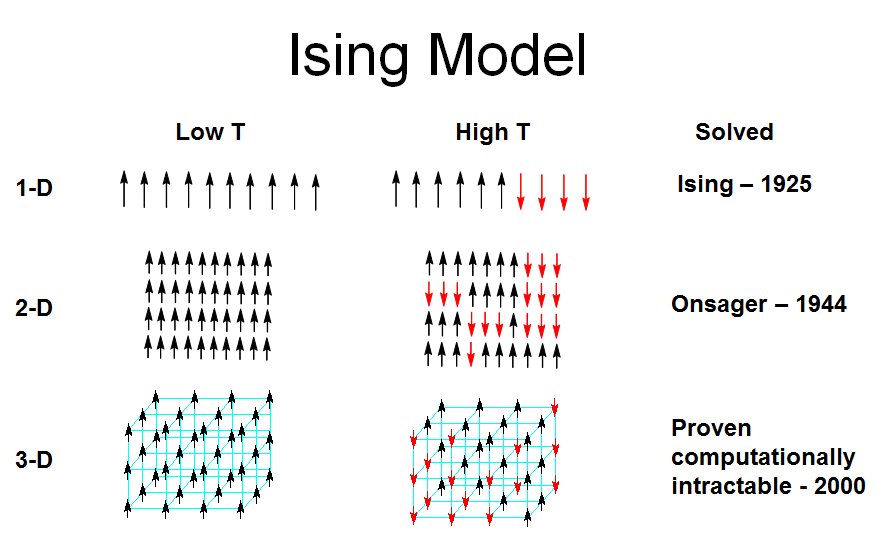
Ising模型中的传递矩阵是通过考虑一维Ising模型的周期性边界条件来构建的。对于一维Ising模型,其哈密顿量可以表示为相邻自旋之间的相互作用。传递矩阵方法将问题转化为求解一个矩阵的本征值问题,其中矩阵的元素对应于不同自旋配置之间的相互作用能量。
传递矩阵的构建过程如下:
- 定义自旋变量,通常取值为+1或-1,代表自旋向上或向下。
- 确定相邻自旋之间的相互作用,即在哈密顿量中相邻自旋乘积的系数。
- 引入周期性边界条件,即首尾自旋也相互作用。
- 构建传递矩阵,其元素对应于不同自旋配置之间的相互作用能量。
- 通过求解传递矩阵的最大本征值来获得配分函数,进而得到系统的热力学量。
传递矩阵的物理意义在于,它提供了一种计算配分函数的方法,从而可以研究系统的热力学性质,如自由能、磁化率和比热容等。通过分析传递矩阵的本征值,可以了解系统的相变行为,例如铁磁相变和顺磁相变。此外,传递矩阵方法也可以推广到更高维度的Ising模型,以及研究其他类型的相变和临界现象。
引用来源: