参考资料

参考资料
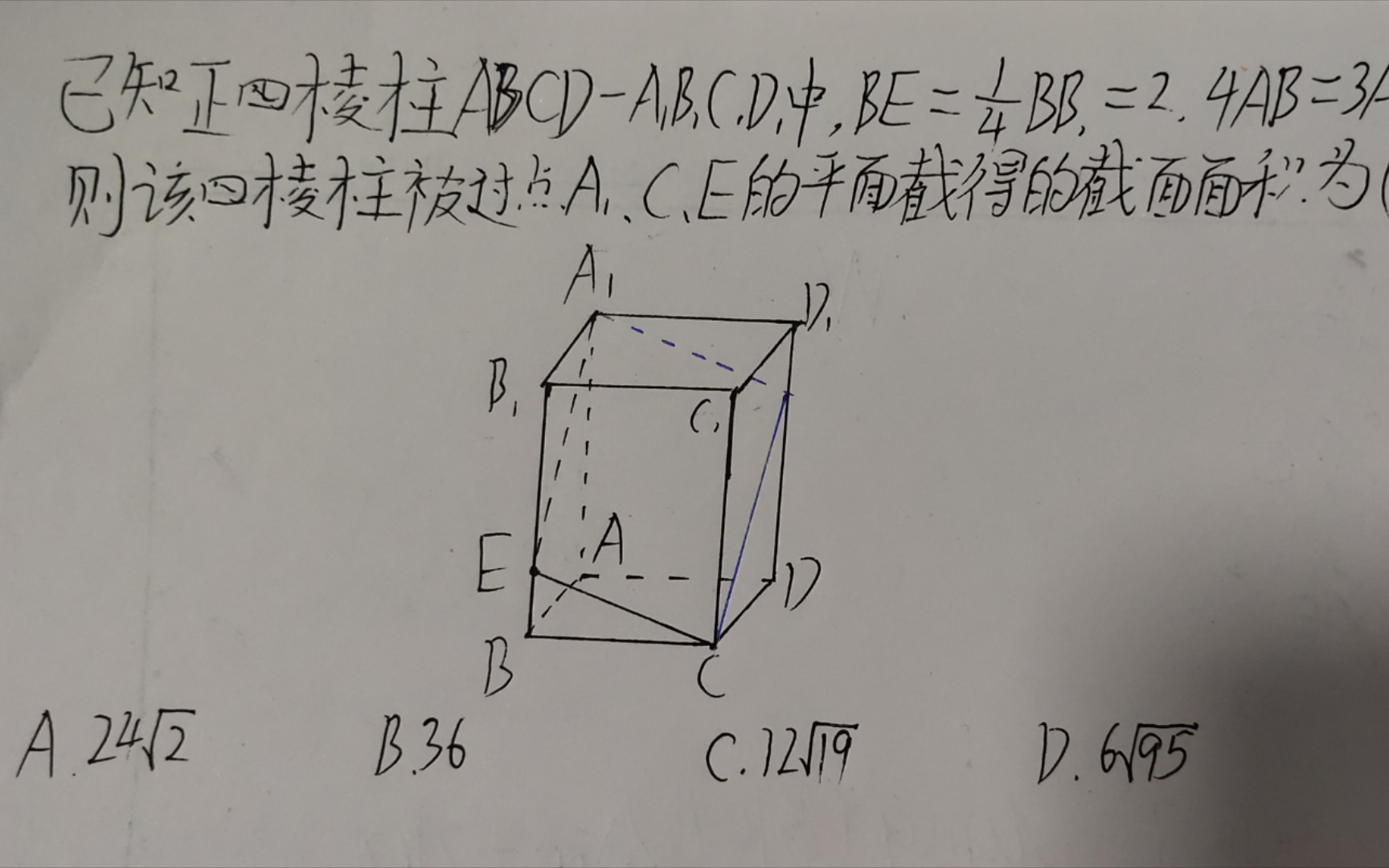
Moonshot回答
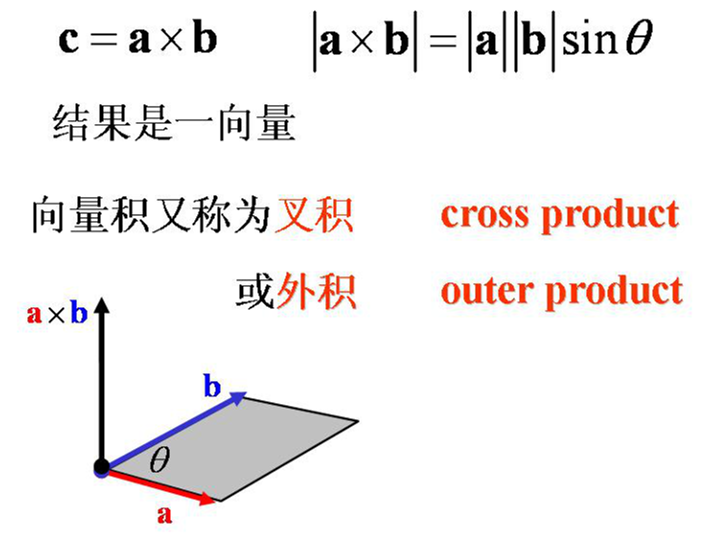
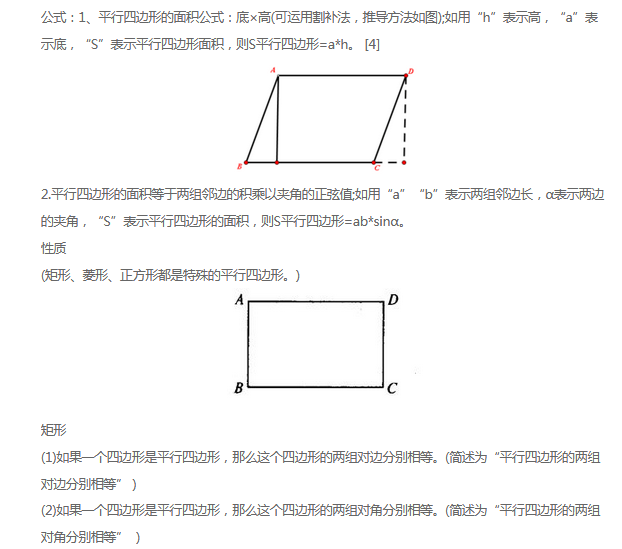
在几何意义上,两个向量的外积(又称为叉乘)与以这两个向量为边构成的平行四边形的面积有直接关系。外积的模长(即结果向量的长度)等于这两个向量构成的平行四边形的面积。具体来说:
-
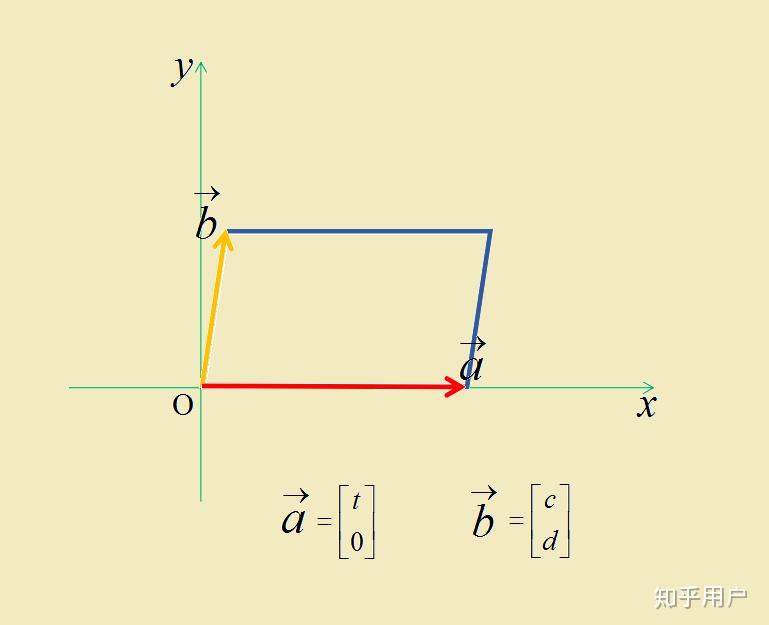
平行四边形面积:如果有两个三维空间中的向量 (\vec{a}) 和 (\vec{b}),它们的外积 (\vec{a} \times \vec{b}) 的模长等于以 (\vec{a}) 和 (\vec{b}) 为相邻边的平行四边形的面积。数学表达式为 (|\vec{a} \times \vec{b}| = |\vec{a}||\vec{b}|\sin(\theta)),其中 (\theta) 是两个向量之间的夹角。
-
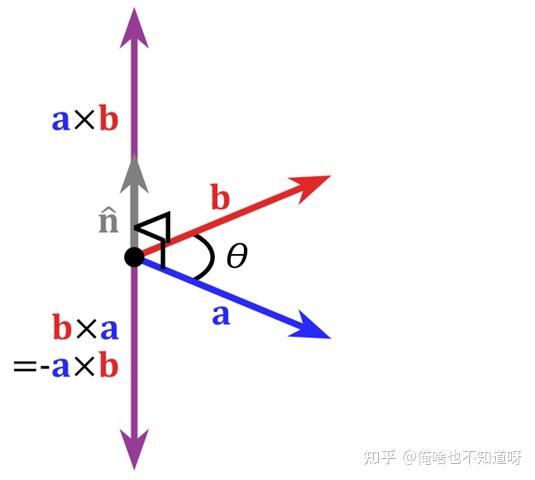
方向:外积结果向量 (\vec{a} \times \vec{b}) 的方向垂直于由 (\vec{a}) 和 (\vec{b}) 构成的平面,并且遵循右手定则。
-
二维情况:对于二维向量,虽然无法直接计算外积,但可以计算两向量张成的平行四边形面积,这可以通过将二维坐标扩充到三维空间并应用外积公式来实现。
-
外积与内积:外积与内积(点积)不同,内积是一个标量,表示两个向量的夹角和它们的大小,而外积是一个向量,表示由两个向量构成的平行四边形的面积和方向。
通过搜索结果,我们可以看到多个来源都支持了上述解释,说明了外积的模长与平行四边形面积的关系,以及外积的方向特性。例如,OI Wiki 中提到外积的几何意义是平行四边形的面积,并且说明了如何通过扩充二维坐标到三维来计算这个面积。此外,知乎专栏中也讨论了外积与平行四边形面积的关系,并提供了详细的计算方法。
继续提问
相关问题
《印度快报》对《惊天营救2》的评价是什么,他们提到的电影的优缺点是什么?
巴巴里奴隶贸易的规模有多大?据估计有多少欧洲人被奴役?
谢伊斯起义如何暴露了邦联条例的缺陷,并推动了美国宪法的制定?
《喀秋莎》这首歌在中国为何如此著名,甚至成为志愿军赴朝参战的军乐?
《黄色大象》这本小说首次出版于哪一年,随后有哪些改编?
Holocaust Denial on Trial项目的主要目标是什么?
阿拉巴马州为何被称为酒精管制州,这对当地居民的生活有何影响?
拜占庭式建筑是如何在古罗马建筑的基础上融合东方艺术,形成独特风格的?
《冷面虎》的片长是多少分钟?
在拜占庭和伊斯兰统治时期,犹太人在巴勒斯坦的生活发生了哪些重大变化?