参考资料

广义相对论中时空弯曲的数学表达式主要通过爱因斯坦场方程（Einstein Field Equations, EFE）来描述。这个方程是一组十个非线性偏微分方程，它们将时空的几何（通过度规张量gμν来描述）与其中的物质和能量（通过应力-能量张量Tμν来描述）联系起来。爱因斯坦场方程的一般形式是：

[ G_{\mu\nu} + \Lambda g_{\mu\nu} = \frac{8\pi G}{c^4} T_{\mu\nu} ]

其中：

• ( G_{\mu\nu} ) 是爱因斯坦张量，它描述了时空的曲率。
• ( \Lambda ) 是宇宙常数，代表空间的固有能量密度。
• ( g_{\mu\nu} ) 是度规张量，它定义了时空的几何结构。
• ( G ) 是引力常数。
• ( c ) 是光速。
• ( T_{\mu\nu} ) 是应力-能量张量，它包含了时空中物质和能量的分布信息。

这个方程的解给出了时空的度规，也就是描述时空弯曲的具体数学表达式。不同的物质和能量分布会导致不同的时空弯曲，因此爱因斯坦场方程的解可以非常复杂。在一些简化的情况下，比如球对称质量分布（如施瓦西解）或旋转质量（如克尔解），可以得到精确的解。在更一般的情况下，可能需要数值方法来求解这些方程。

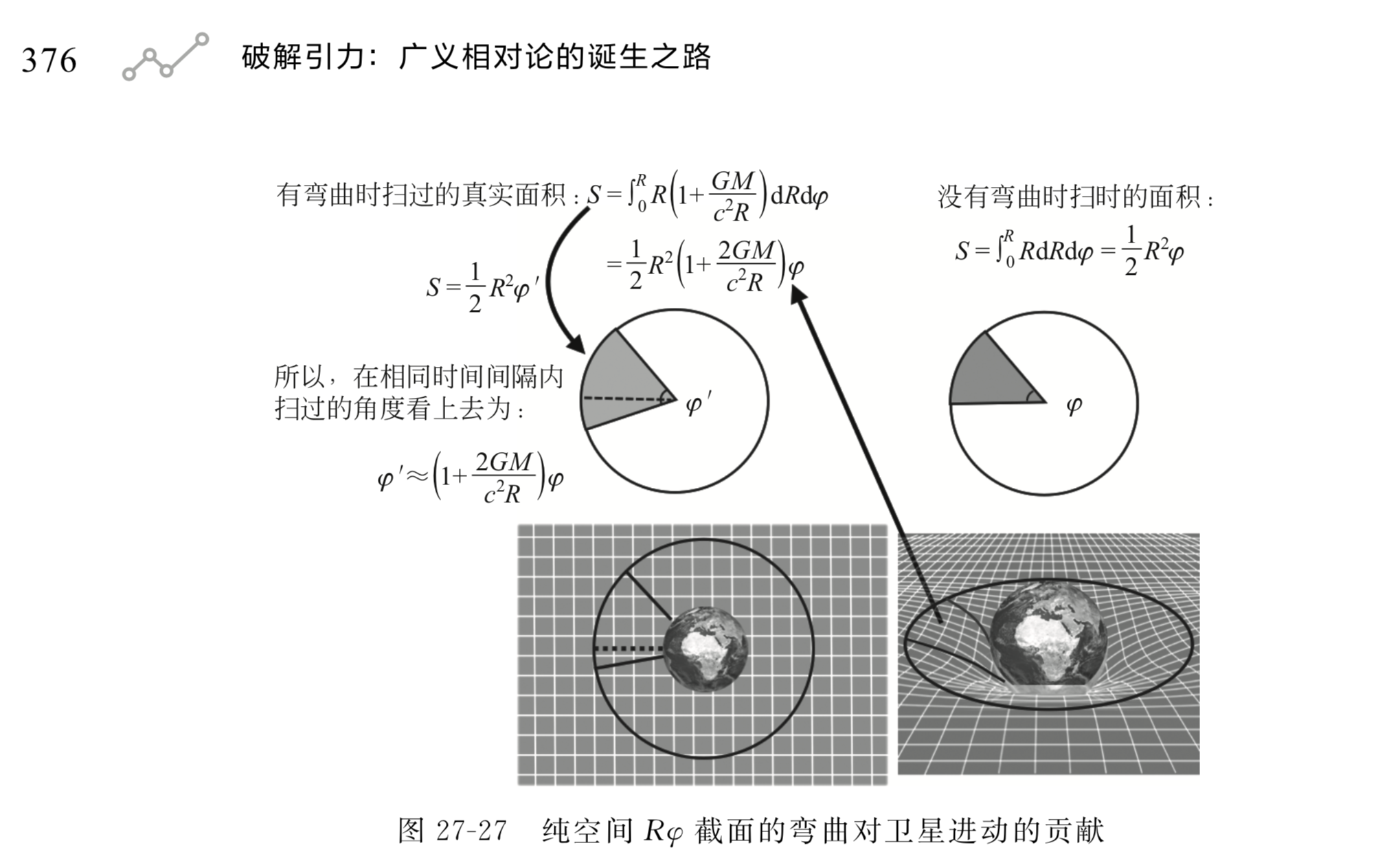
图片展示了时空几何与引力理论的关系，其中强调了广义相对论中无挠率的黎曼时空的重要性。来源