作用量-角度坐标如何在哈密顿力学中用于处理非线性微扰问题?
参考资料
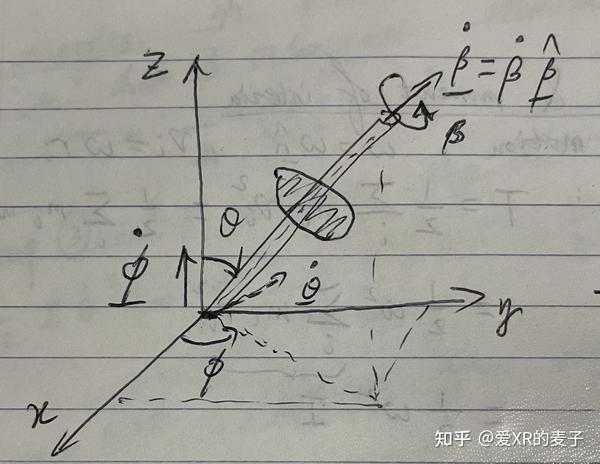


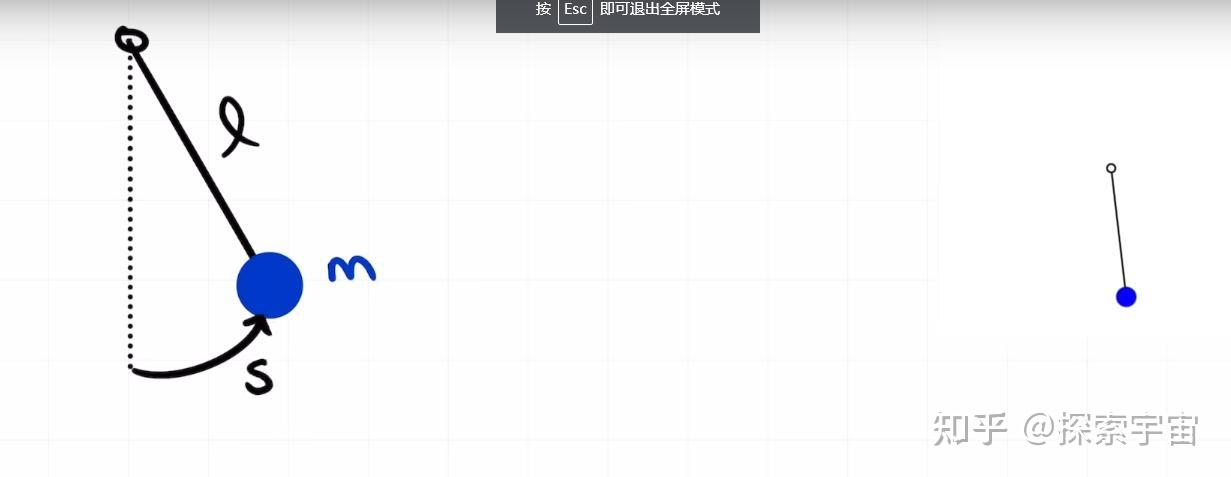
Moonshot回答
在哈密顿力学中,作用量-角度坐标是处理非线性微扰问题的一种有效方法。通过使用这些坐标,可以简化系统的动力学分析,尤其是在研究可积系统和微扰理论时。作用量-角度坐标允许我们绕过解析运动方程式,直接求得振动或旋转的频率。
KAM定理是研究非线性微扰问题时的关键结果,它表明对于微小的微扰,环面不变量是稳定的。这意味着在一定条件下,系统的动力学行为在微扰下仍然保持不变。这一定理在混沌理论的研究中具有重要意义。
此外,作用量-角度坐标也用于完全可分的哈密顿-亚可比方程式,其中哈密顿量显性地不含时间。这使得我们能够更深入地理解系统的动力学特性,尤其是在处理非线性微扰时。
以下是一些与作用量-角度坐标相关的图像,可以帮助直观理解这一概念:



这些图像展示了作用量-角度坐标在描述系统动力学行为时的直观性和有效性。通过这些图像,我们可以更好地理解作用量-角度坐标在哈密顿力学中的应用,尤其是在处理非线性微扰问题时。更多详细信息可以参考维基百科上的作用量-角度坐标条目。