流体动力学中的伯努利方程在什么情况下适用,它描述了流体有哪些物理量之间的关系?
参考资料




参考资料


Moonshot回答
伯努利方程在流体动力学中描述了流体的静压、动压和势能之间的关系。它适用于以下条件:
- 流体是不可压缩的,即流体的密度保持不变。
- 流动是定常的,即流体在任何一点的性质不随时间改变。
- 流动是无粘性的,即不考虑流体的粘性。
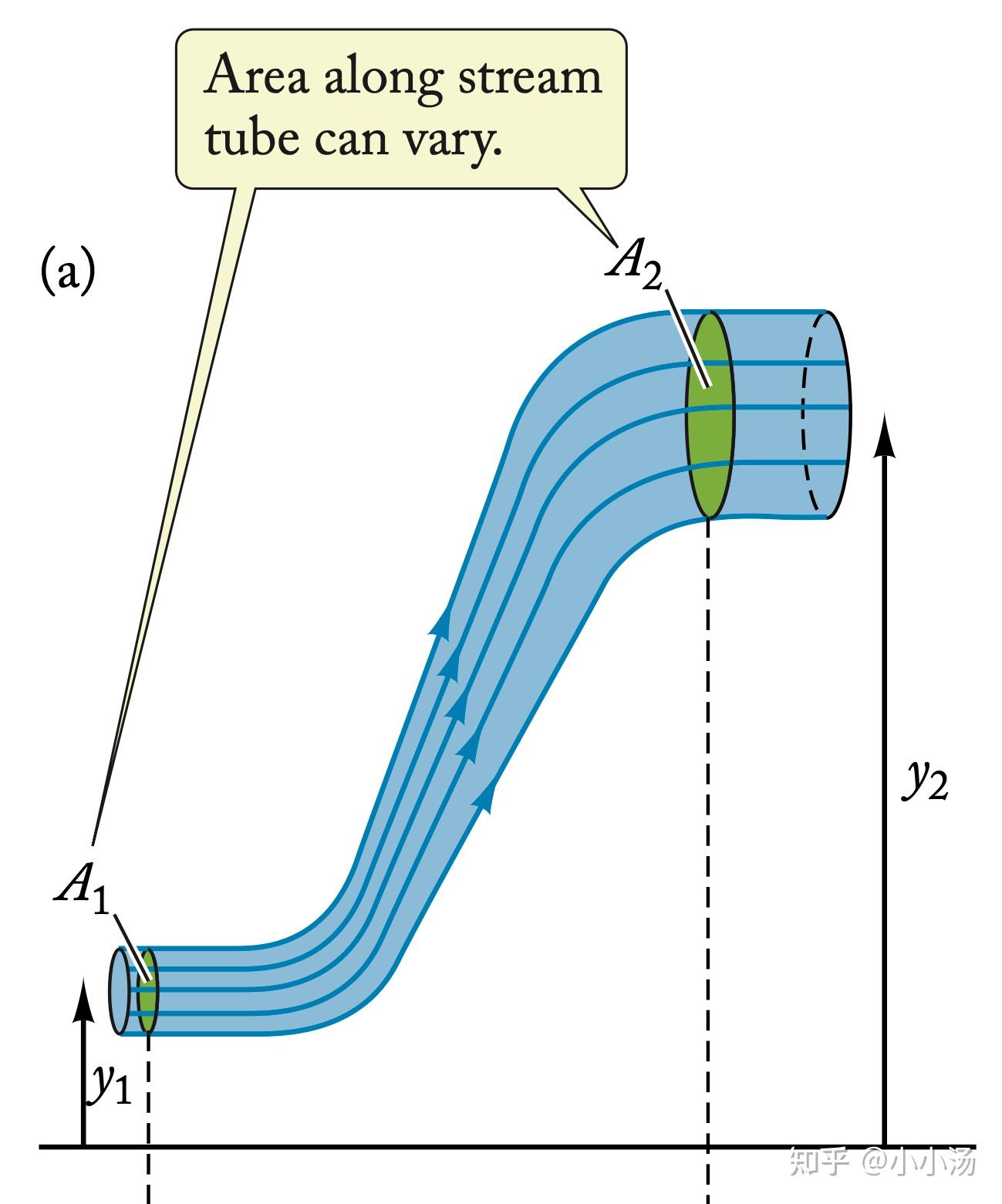
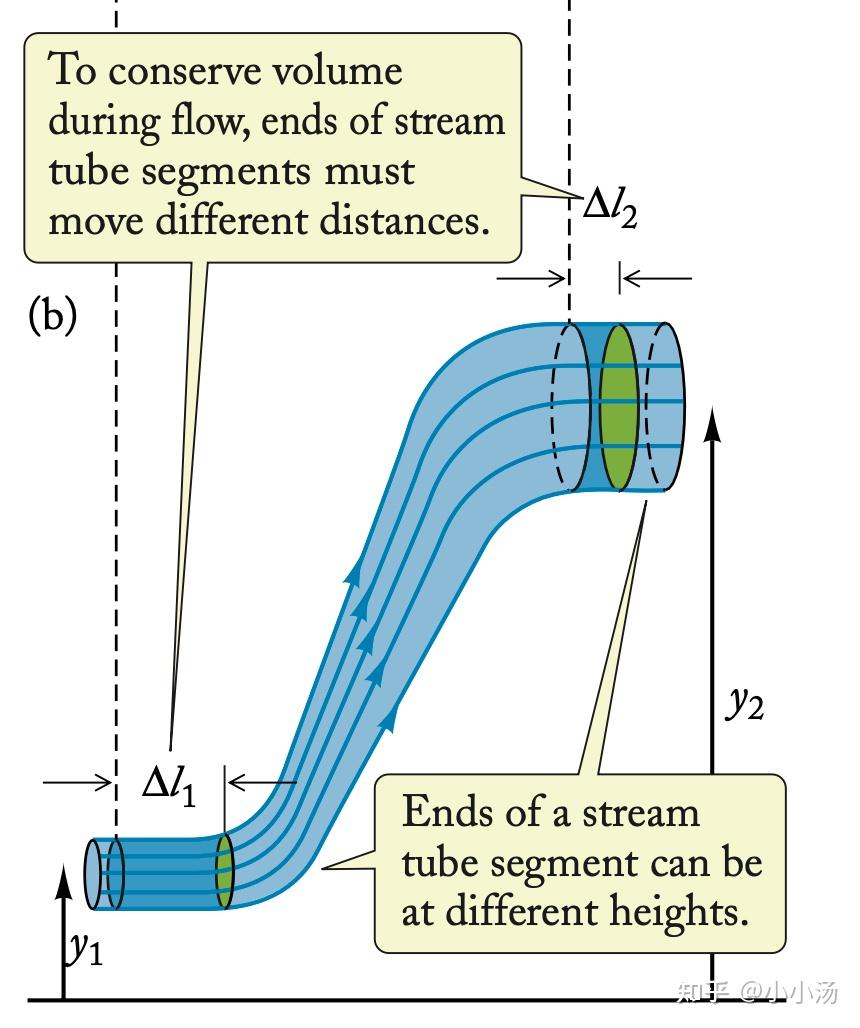
- 流动是沿流线的,即在流线上的任意两点之间,流体的总能量(包括压力能、动能和势能)是守恒的。
伯努利方程的数学表达式为: [ P + \frac{1}{2} \rho v^2 + \rho gh = \text{常数} ] 其中,(P) 是流体的静压,(\rho) 是流体的密度,(v) 是流体的速度,(g) 是重力加速度,(h) 是流体相对于某个参考水平面的高度。

这个方程表明,在没有粘性损失的理想流体流动中,流体的总能量沿流线是守恒的。这意味着,当流体的速度增加时,其压力会减小;反之,当流体的速度减小时,其压力会增加。这种关系在流体力学的许多应用中都非常重要,例如飞机机翼的设计和管道系统中流体的流动分析。