参考资料

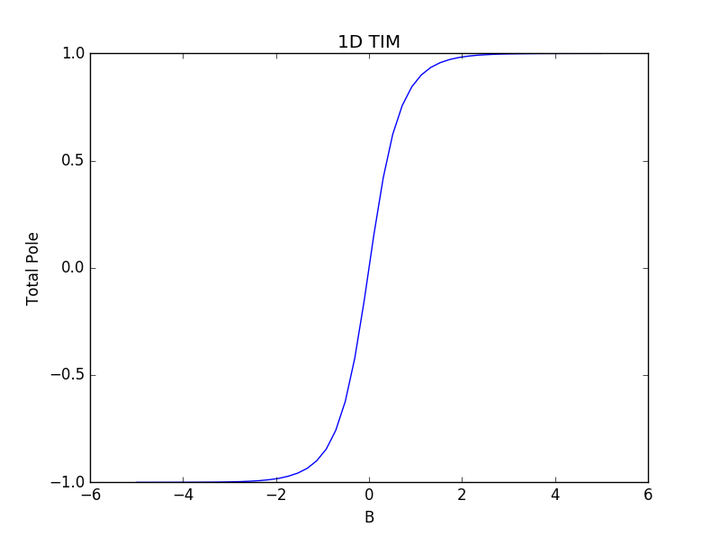
易辛模型（Ising Model）是统计物理学中一个非常重要的模型，它最初由Wilhelm Lenz于1920年提出，并由他的学生Ernst Ising进一步发展，用来描述铁磁性材料内部原子自旋的排列以及它们与宏观磁化强度之间的关系。这个模型虽然简单，却能提供丰富的物理内容，并且可以成功地解释铁磁和顺磁态之间的相变。

易辛模型在统计物理中的应用非常广泛，包括但不限于：

1. 解释磁场现象：易辛模型可以模拟铁磁性物质的结构，并对铁磁性状态和非铁磁性状态之间的相变进行理论描述。例如，当铁磁性物质的温度低于居里温度时，其内部的原子会按特定方式自旋从而产生宏观磁矩。

2. 临界现象和相变研究：易辛模型可以用来研究物质在不同相态之间的转变，如液体到气体的相变，以及这些转变过程中的临界现象。

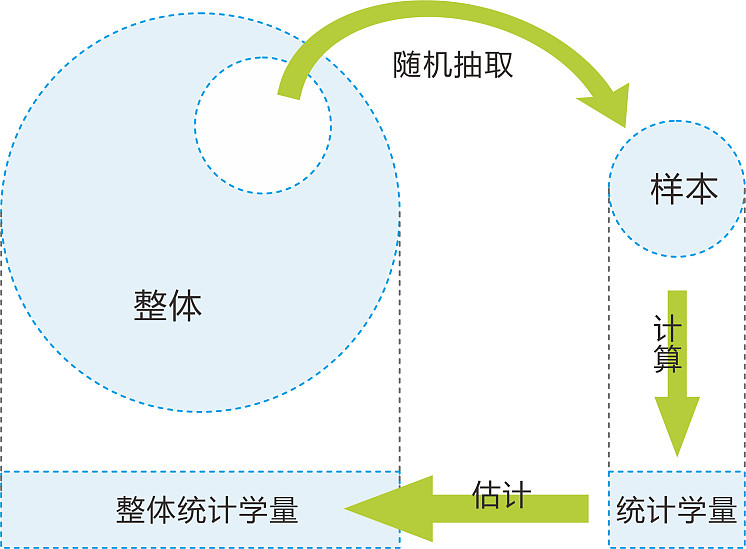
3. 普适性研究：易辛模型展示了系统中个体状态与宏观状态之间的关系，并且具有普适性，即不同物质在相变发生时，都有着相同的临界指数。

4. 其他学科的应用：易辛模型的概念也被应用到其他领域，如DNA的折叠、病毒的传播、大脑神经细胞的激活状态等，这些领域中都存在着有序与无序的相变和临界现象。

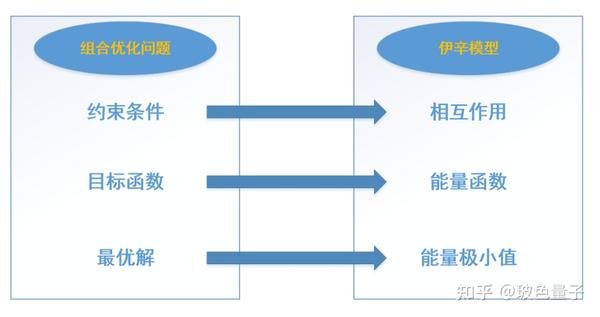
5. 社会和经济物理学：易辛模型还推动了社会物理学和经济物理学的发展，因为社会和经济行为同样由众多个体组成，这些个体之间相互影响，并受到宏观因素的影响。

此外，易辛模型在理论发展上也具有重要意义，比如它在二维和三维情况下的精确解的获得，以及在研究量子相变和临界现象时的新方法的提出，都显示了这个模型的深远影响。例如，西湖大学理学院朱伟团队在三维伊辛模型的研究中取得了重大进展，提出了一种新的理论方法用以研究相变及临界现象，这种方法可能为理解临界现象打开一个新的维度。