符号动力学在实际生活中有没有应用实例,比如在信息编码或图像处理领域?
参考资料
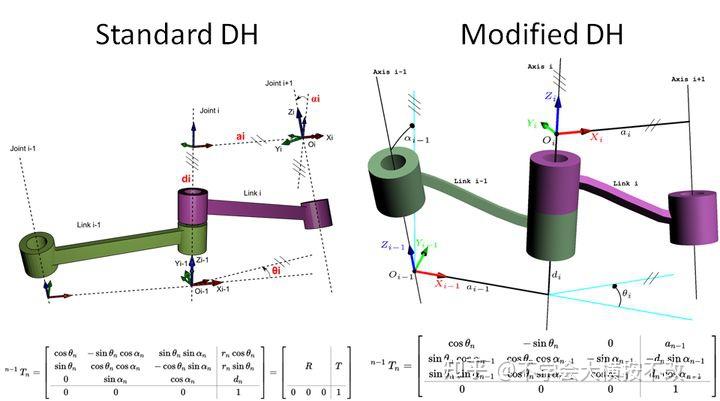

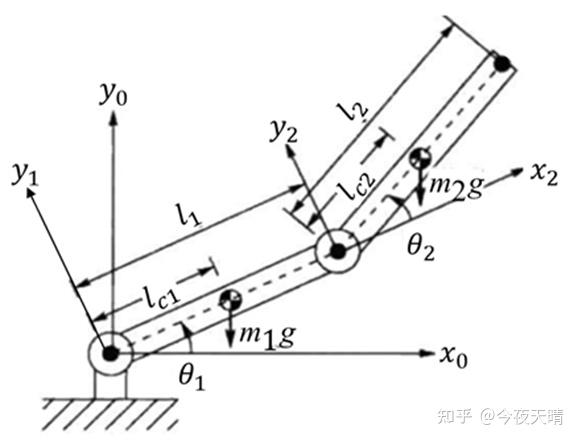
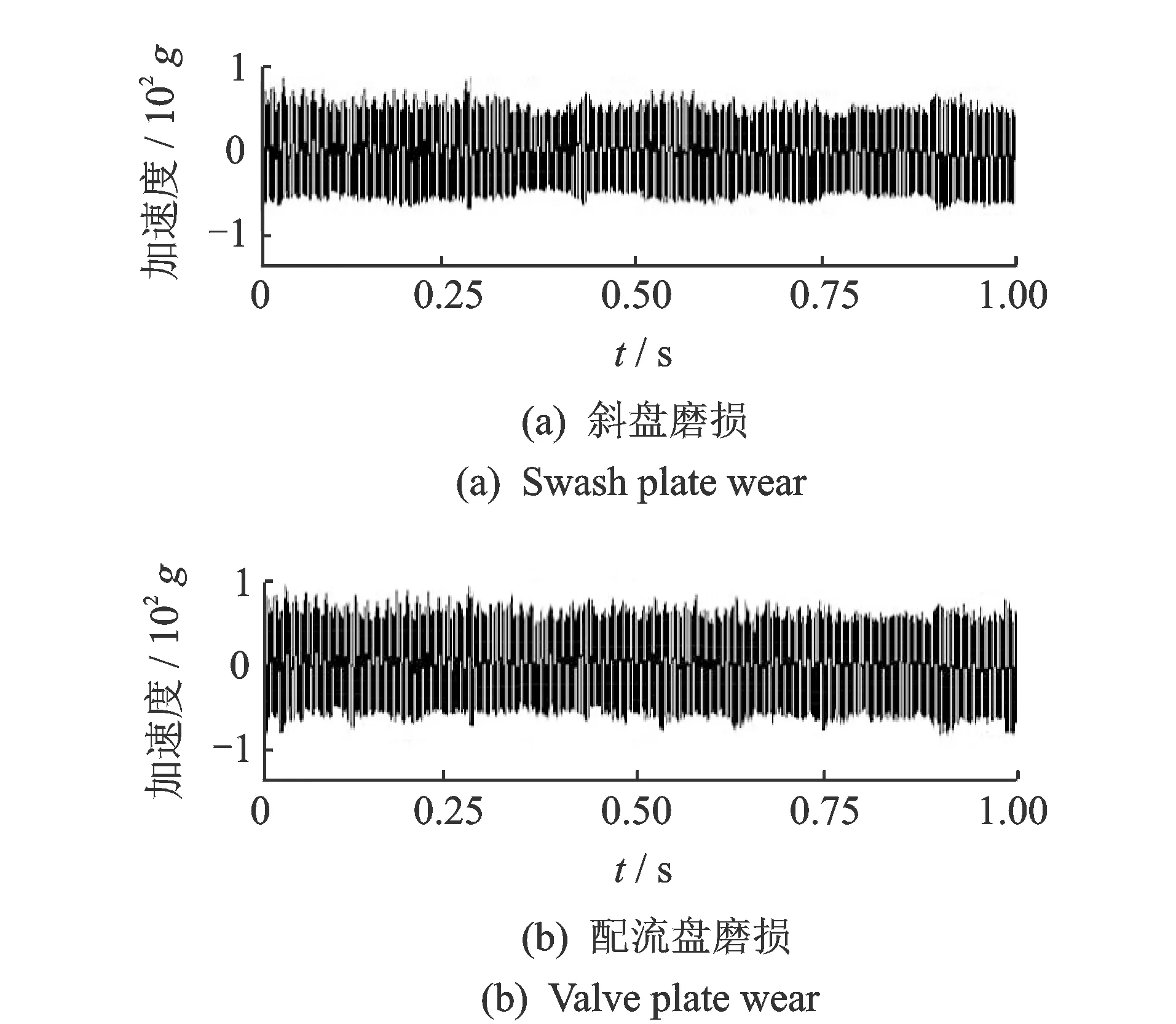
参考资料
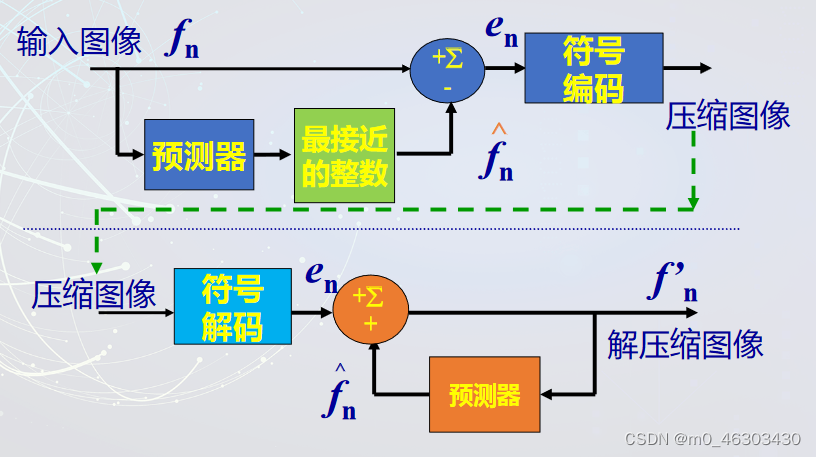


Moonshot回答
符号动力学在实际生活中确实有应用实例,特别是在信息编码和图像处理领域。以下是一些具体的应用案例:
-
信息编码:符号动力学可以用于分类动力系统,将动力系统何时与另一个动力系统“等价”的问题,通过符号动力学,变成了一个编码问题。这种方法可以用于信息编码,通过将信息转换为符号序列,进而分析和处理这些信息。
-
图像处理:在图像处理领域,符号动力学可以用于分析图像的复杂度和结构。例如,通过将图像转换为符号序列,可以研究图像的动力学特性,进而用于图像的分类、识别和重建。
-
脑电信号处理:符号动力学分析及其在脑电信号处理中的应用,可以帮助分析脑电信号的复杂度,进而用于脑疾病的诊断和治疗。
-
混沌伪随机序列:符号动力学的方法也可用于分析混沌伪随机序列的复杂度,这在信息安全领域有重要应用,因为混沌伪随机序列可以用于生成高质量的密钥。
-
认知事件相关电位分析:符号动力学还被用于分析认知事件相关电位的复杂度,这有助于研究大脑的认知过程。
-
神经符号学:神经符号学的基本方法是构建一个准符号空间,该空间具备语义信息和连续性,这在信息编码和图像处理中都有应用。
这些应用展示了符号动力学在不同领域的广泛潜力,尤其是在处理复杂系统和信号时。通过将复杂的信息转换为符号序列,符号动力学为分析和理解这些复杂系统提供了一个有力的工具。