在量子力学中,波函数的归一化是什么意思,又为什么是必要的?
参考资料

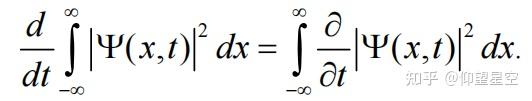
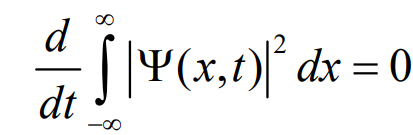
Moonshot回答
在量子力学中,波函数的归一化是一个非常重要的概念。归一化意味着波函数的模平方在全空间的积分等于1,这保证了波函数具有概率密度的物理意义。具体来说,波函数的模平方 |Ψ(x,t)|^2 表示粒子在时刻 t 和位置 x 附近出现的概率密度。因此,通过归一化处理,我们可以确保在全空间找到粒子的概率总和为1,即粒子必定存在于空间中的某处。
归一化的必要性在于,它确保了量子力学的预测与概率论的基本原则相一致。没有归一化的波函数无法直接用于计算粒子出现在特定位置的概率。此外,归一化还有助于保证量子力学中的物理量,如能量和动量,具有明确和一致的物理意义。
归一化操作是合理的,因为任何波函数都可以乘以一个常数而仍然是薛定谔方程的解。因此,通过乘以一个适当的常数(归一化系数),我们可以将波函数归一化,使其满足归一化条件。在实际应用中,即使给出的波函数没有明确归一化,只要相对概率分布是正确的,我们仍然可以通过引入归一化系数来调整。
总的来说,波函数的归一化是量子力学中的一项基本要求,它确保了波函数的概率解释与物理现象的一致性。通过归一化,我们可以更准确地描述和预测粒子的行为,这是理解和应用量子力学的关键步骤。