什么是几何积在几何代数中是如何定义的,它与其他代数操作有何不同?
参考资料

参考资料


Moonshot回答
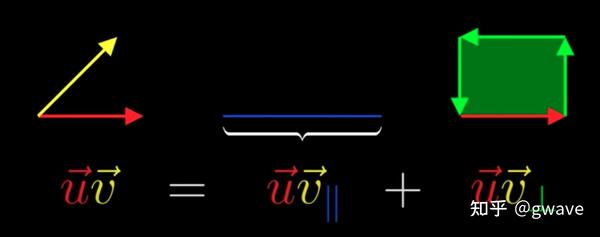
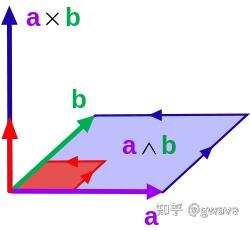
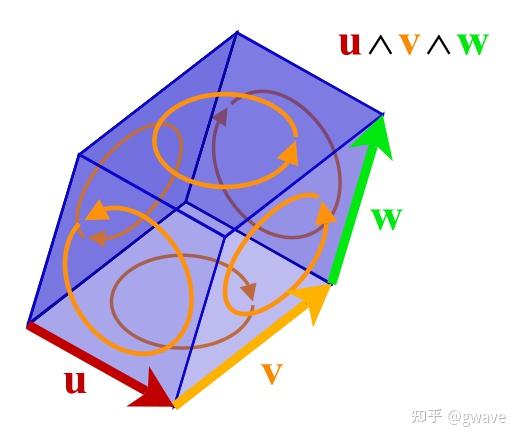
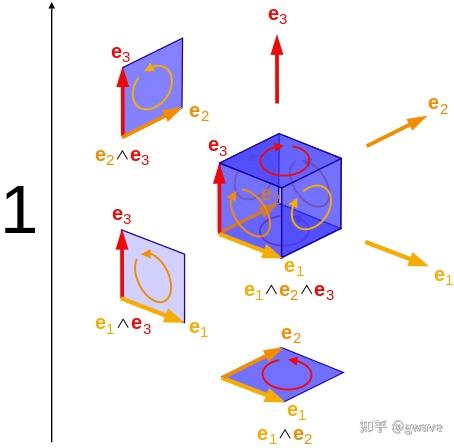
几何积在几何代数中的定义是将向量乘积的概念扩展到更高维度的对象,称为多重向量。它由加法和几何积两种基本运算组成,其中几何积结合了内积和外积两种运算,是复数代数、四元数代数和外代数的推广。几何积不仅包括向量间的点积,还包含向量的外积,这使得它能够表达更丰富的几何关系。
几何积与其他代数操作的主要区别在于:
-
几何直观性:几何积蕴含着丰富的几何意义,能够直接表达向量之间的几何关系,如平行、垂直等,而传统代数操作如矩阵乘法则缺乏这种直观性。
-
维度处理:几何代数支持不同维度对象的向量除法与加法,而传统代数如矩阵代数在处理不同维度对象时会遇到更多限制。
-
统一性:几何代数统一了多种数学结构,如四元数、矩阵代数、复数等,提供了一个更为统一的数学框架来描述物理现象。
-
计算效率:在某些情况下,使用几何积可以简化计算过程,因为它允许使用更少的公式和概念来表达复杂的几何关系。
几何代数的这些特性使其在物理学、计算机图形学等领域有着广泛的应用。例如,在描述空间中的旋转和提升时,几何代数提供了一种更为简洁和强大的工具。通过几何积,可以以一种直观和高效的方式处理多维空间中的几何问题。