哈密顿-雅可比方程的主要应用是什么?
参考资料

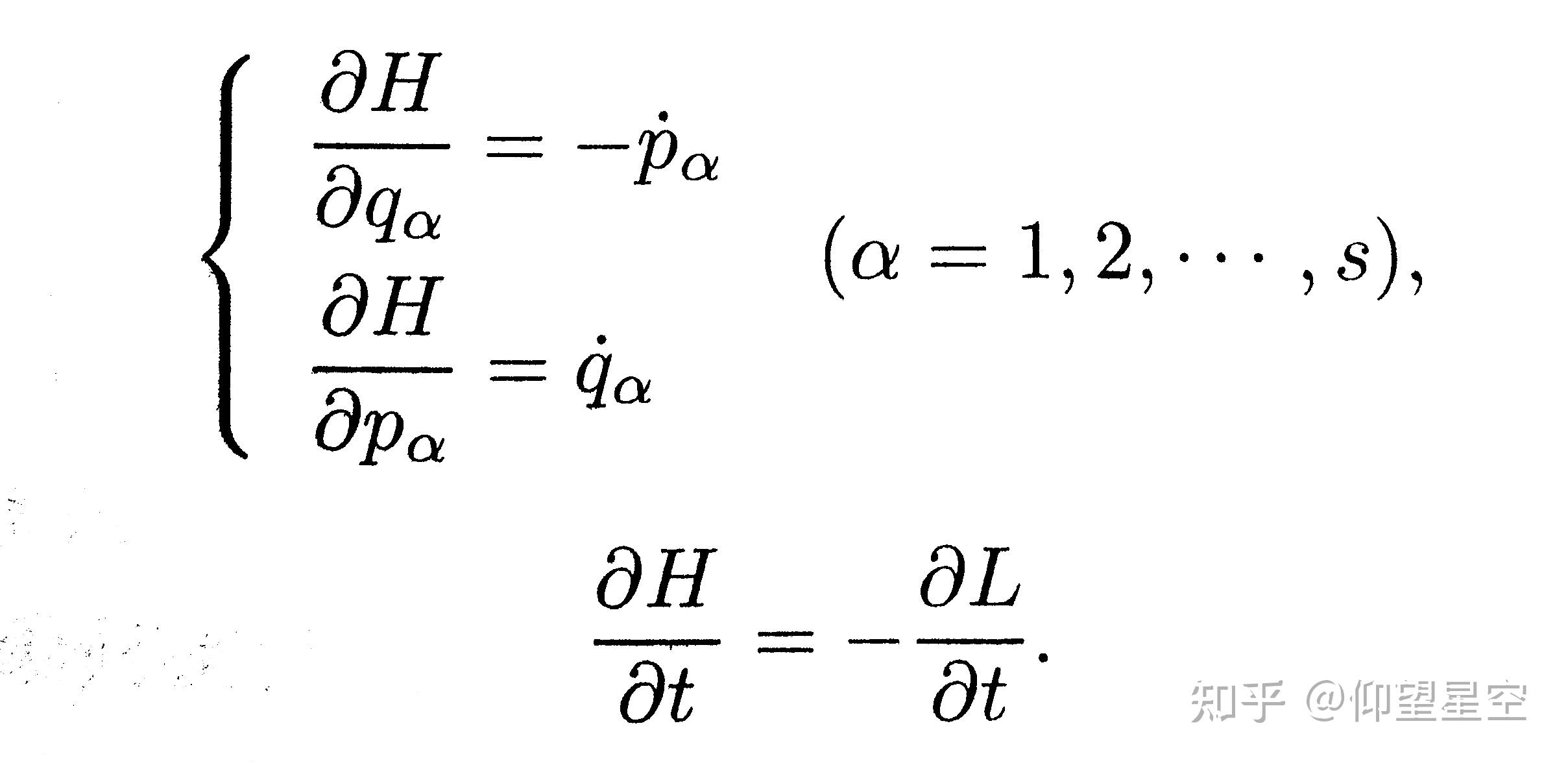


Moonshot回答
哈密顿-雅可比方程的主要应用包括:
-
经典力学系统的行为描述:哈密顿-雅可比方程是一个一阶非线性偏微分方程,其解描述了系统的行为。它与哈密顿方程不同之处在于,哈密顿-雅可比方程是一个偏微分方程,每个变量对应于一个坐标,而哈密顿方程是一个一组一阶常微分方程。
-
最优控制理论:在最优控制领域,哈密顿-雅可比方程用于寻找最小成本的控制实值函数。哈密顿-雅可比-贝尔曼方程(HJB方程)是该领域的中心,它是一个偏微分方程,用于求解特定动态系统及相关成本函数下的最优控制策略。
-
量子力学和波动力学:哈密顿-雅可比方程在量子力学中也有应用,特别是在半经典近似中,它有助于理解量子系统的行为。
-
几何光学:哈密顿-雅可比方程可以描述光的物理行为,包括衍射、干涉等现象,这些现象无法用纯几何光学完全解释。
-
相对论物理学:在相对论物理学中,哈密顿-雅可比方法被用来求解电子在激光场中的相对论性运动方程,并在不同的参照系中得到解析表达式。
-
动态博弈:在动态博弈中,哈密顿-雅可比方程也会出现,用于分析和解决博弈问题。
这些应用展示了哈密顿-雅可比方程在物理学和工程学中的广泛适用性,它为理解和预测复杂系统的行为提供了一个强大的工具。