参考资料

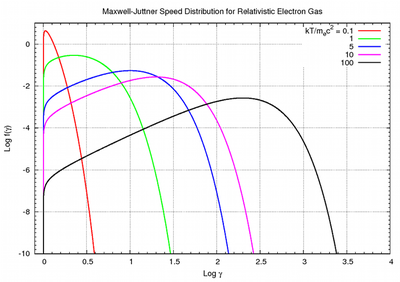
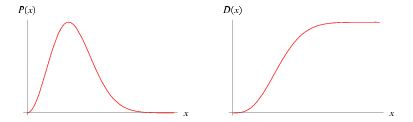
麦克斯韦-玻尔兹曼分布函数在玻尔兹曼方程中扮演着至关重要的角色。它描述了理想气体分子的速率分布，具体说明了气体分子在不同速度上的比例，作为系统温度的函数。这个分布函数解释了许多基本的气体性质，包括压强和扩散。在统计力学中，麦克斯韦-玻尔兹曼分布形成了分子运动论的基础，它对应于由大量不相互作用的粒子所组成的系统中最有可能的速率分布，其中量子效应可以忽略。

玻尔兹曼方程是一个描述气体分子运动的动力学方程，而麦克斯韦-玻尔兹曼分布函数提供了玻尔兹曼方程在统计力学框架下的微观解释。它展示了气体分子在平衡状态下的速度分布，帮助我们理解气体分子的动力学行为和热力学性质。通过这个分布函数，我们可以推导出气体的输运系数，如粘滞度和热导率，这些都是研究气体动力学和热力学性质的重要参数。

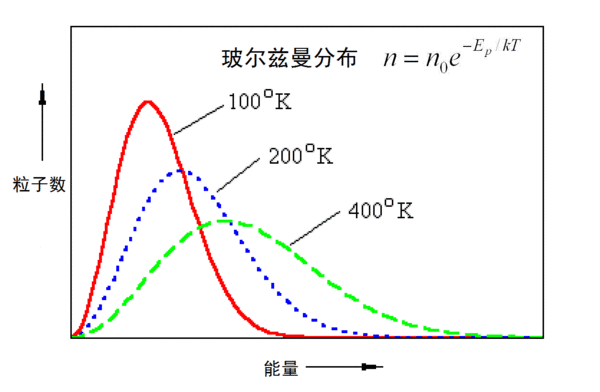
此外，麦克斯韦-玻尔兹曼分布函数还与玻尔兹曼分布有关，后者是统计力学中描述粒子在不同能量状态上的分布的定律。玻尔兹曼分布是麦克斯韦-玻尔兹曼分布的一个特例，当考虑分子的能量分布而非速度分布时适用。

综上所述，麦克斯韦-玻尔兹曼分布函数在玻尔兹曼方程中的作用是提供了一个统计描述，帮助我们理解和预测气体分子在不同条件下的行为和性质。它与玻尔兹曼分布一起，构成了理解和分析气体分子运动及宏观性质的基础。