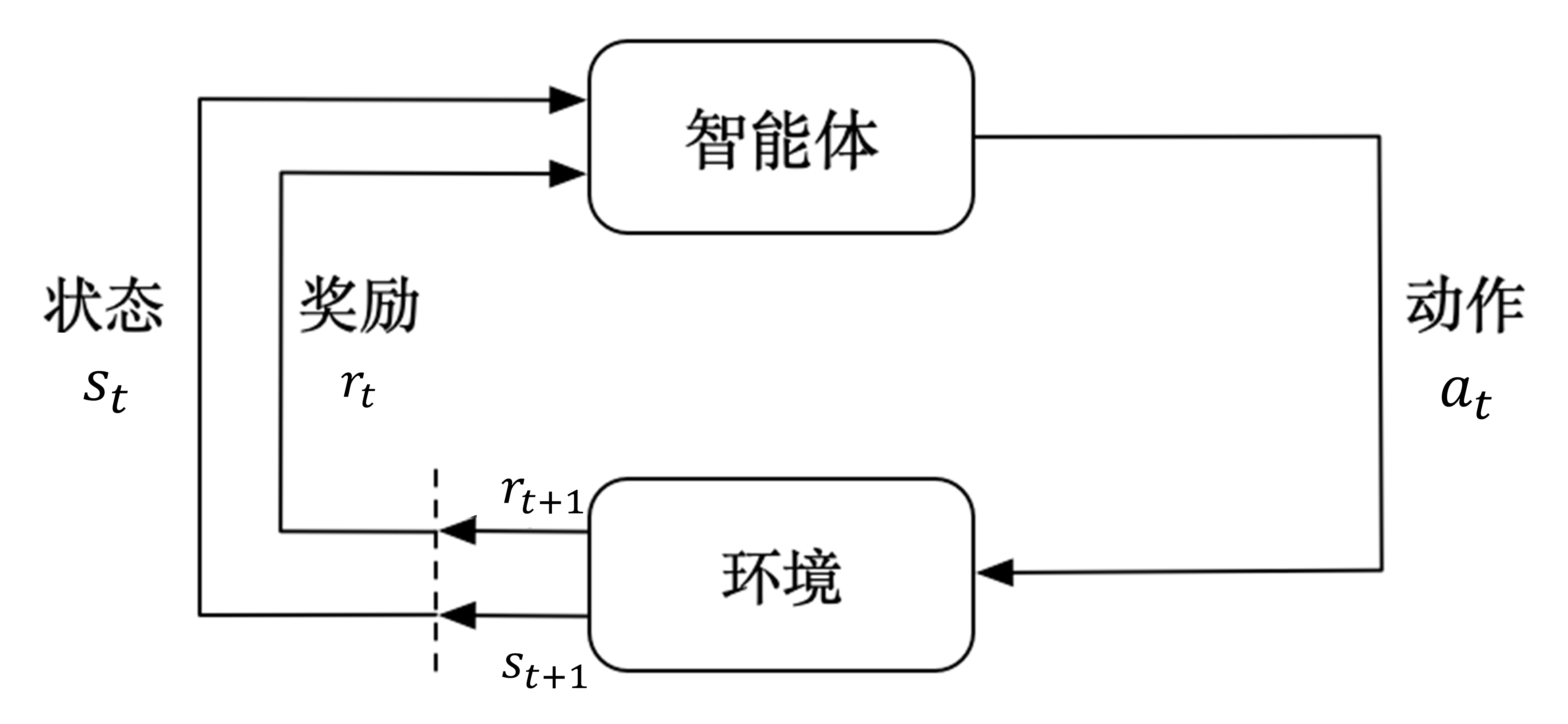
参考资料



参考资料


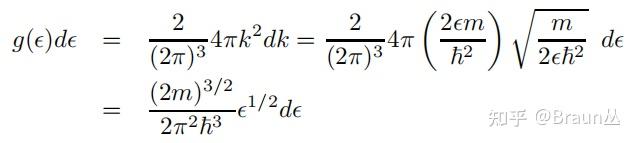
Moonshot回答
贝特-萨尔皮特方程(Bethe-Salpeter Equation, BSE)确实在凝聚态物理领域有应用,尤其在研究多体系统和电子结构方面。以下是一些具体的应用方面:
-
激子和电子-空穴对:BSE在描述半导体和绝缘体中的激子和电子-空穴对等束缚态方面有广泛应用。例如,复旦大学信息科学与工程学院的研究团队利用BSE研究了二维碲烯的激子光电特性与宏观凝聚全景相图,发现考虑自旋轨道耦合效应时,碲烯中的准粒子带隙被重整化12。
-
多体系统的格林函数:BSE提供了一种计算多体系统的格林函数的方法,这对于理解固体材料中的电子关联效应至关重要。
-
谱方法:BSE与谱Dyson-Schwinger方程技术结合,用于解决束缚态光谱问题,这在处理其他复杂物理系统时可能同样有效,具有广泛的应用前景3。
-
超导体和磁性材料:BSE也用于研究超导体的配对机制和磁性材料中的自旋波等。
-
强关联电子系统:在强关联电子系统中,BSE有助于研究电子之间的强相互作用和集体激发模式。
通过这些应用,我们可以看到BSE在凝聚态物理中的重要性,它为理解和预测材料的电子性质提供了一个强大的理论工具。

Footnotes
继续提问
相关问题
萩名快伸在创作电影《你在天空彼岸》时,有没有受到其他作品的启发或影响,具体体现在哪些方面?
大爆炸理论在科学方法论上有哪些示范性作用,具体体现在哪些方面?
在巴比伦被掳期间,犹太人如何保持他们的宗教和文化传统?
贝特–萨尔皮特方程与其他描述相对论束缚态的方程(比如Dirac方程)相比有什么优缺点?
《惊天营救2》的导演和主要演员是谁,他们在续集中回归情况如何?
任达华饰演的Leon在与Anna发展恋情后,最终为何会遇见恶魔版的Anna?
通过自我意识和自我评价格如何影响一个人成功的程度和方向,有哪些科学依据支撑这种观点?
威斯敏斯特教堂在英格兰的罗马式建筑中有着怎样的重要地位?
历史上有哪些著名的会战实例?
反共主义是如何在全球范围内兴起的?