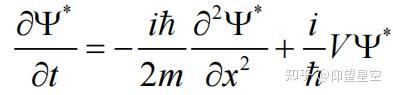什么是波函数的归一化条件及其重要性是什么?
参考资料
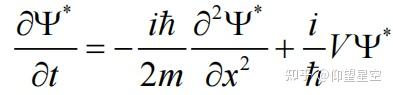
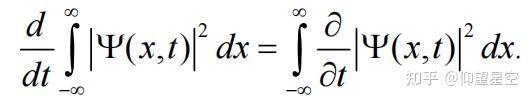
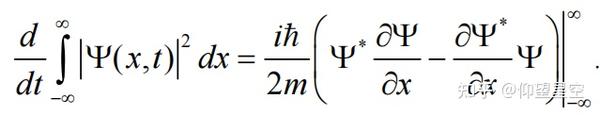
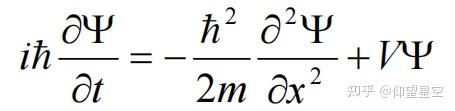
参考资料
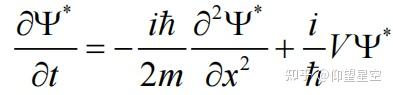
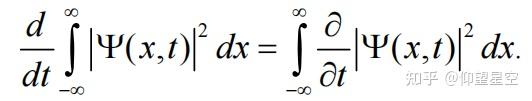
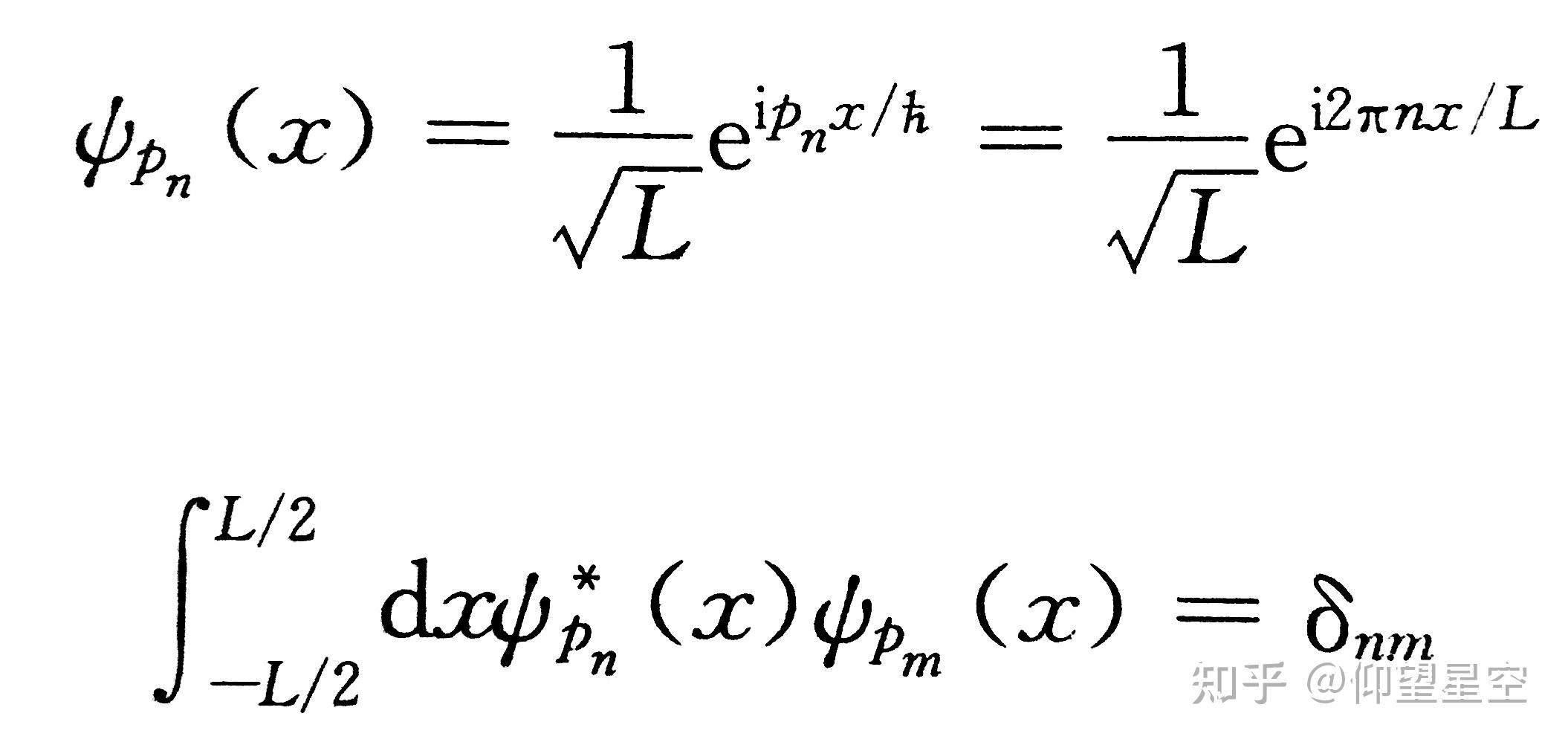
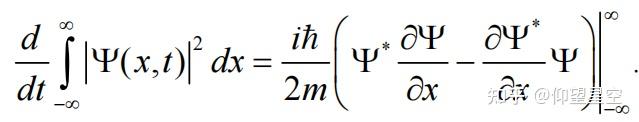
Moonshot回答
波函数的归一化条件是量子力学中的一个基本概念,它要求波函数的模平方在整个空间的积分等于1。数学上表达为:
[ \int_{-\infty}^{+\infty} |\psi(x)|^2 dx = 1 ]
这个条件的重要性在于:
- 概率密度:归一化条件保证了波函数的模平方具有概率密度的物理意义,即粒子在某个位置找到的概率是确定的。
- 总概率为1:它确保了在整个空间内找到粒子的总概率为1,这与概率论的基本原则相符。
- 物理意义:归一化波函数的模平方可以被解释为粒子在特定位置出现的概率密度,这是量子力学描述粒子状态的核心。
- 相对概率:在量子力学中,虽然归一化条件是默认的,但相对概率分布才是研究的重点,即粒子在不同位置出现的概率比例。
归一化条件是量子力学中波函数计算和解释的基础,它使得波函数的数学形式与物理现象——粒子的概率性行为——之间有了直接的联系。通过归一化,我们可以计算粒子在特定状态下的各种物理量,如能量、动量等,这些计算都依赖于波函数的归一化。