参考资料

正弦-戈尔登方程和Thirring模型在理论物理中都非常重要，并且它们之间存在深刻的联系和对偶性。正弦-戈尔登方程是一种经典的非线性偏微分方程，其孤立子解在物理学中具有重要意义。Thirring模型是一个相对论性量子场论模型，用于研究粒子的相互作用和质量的重整化。

正弦-戈尔登方程的拉格朗日量可以写为： [ \mathcal{L} = \frac{1}{2} (\partial_\mu \phi) (\partial^\mu \phi) - \frac{\mu^2}{\beta^2} \cos(\beta \phi) ] 其中，$\phi$ 是一个标量场，$\mu$ 是质量参数，$\beta$ 是一个常数。

Thirring模型是一个描述无质量费米子自相互作用的量子场论模型。其拉格朗日量为： [ \mathcal{L} = \bar{\psi}(i\gamma^\mu\partial_\mu - m)\psi - \frac{1}{2} g (\bar{\psi}\gamma^\mu\psi)(\bar{\psi}\gamma_\mu\psi) ] 其中，$\psi$ 是费米子场，$m$ 是质量，$g$ 是耦合常数。

这两个模型之间的对偶性可以通过Bethe ansatz方法来研究。在某些情况下，Thirring模型可以映射到正弦-戈尔登方程，从而允许使用正弦-戈尔登方程的解来研究Thirring模型的性质。这种对偶性在研究量子场论和统计物理中的非微扰效应时非常有用。

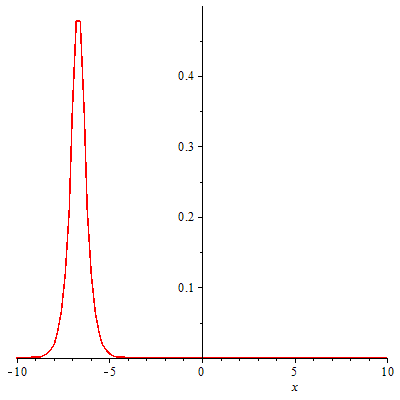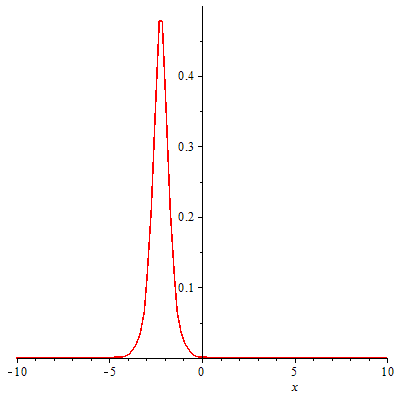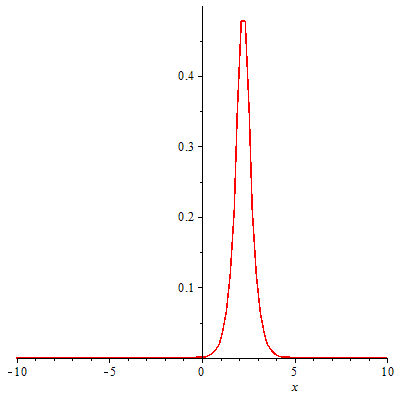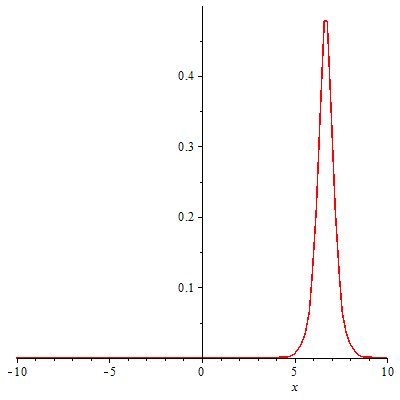
此外，正弦-戈尔登方程的孤立子解和Thirring模型的费米子激发之间也存在对应关系。这种对应关系为理解高能物理和凝聚态物理中的非微扰现象提供了一个有力的工具。