幺正算符在群论中的应用,特别是在Hilb(H)群中的作用是什么?
参考资料

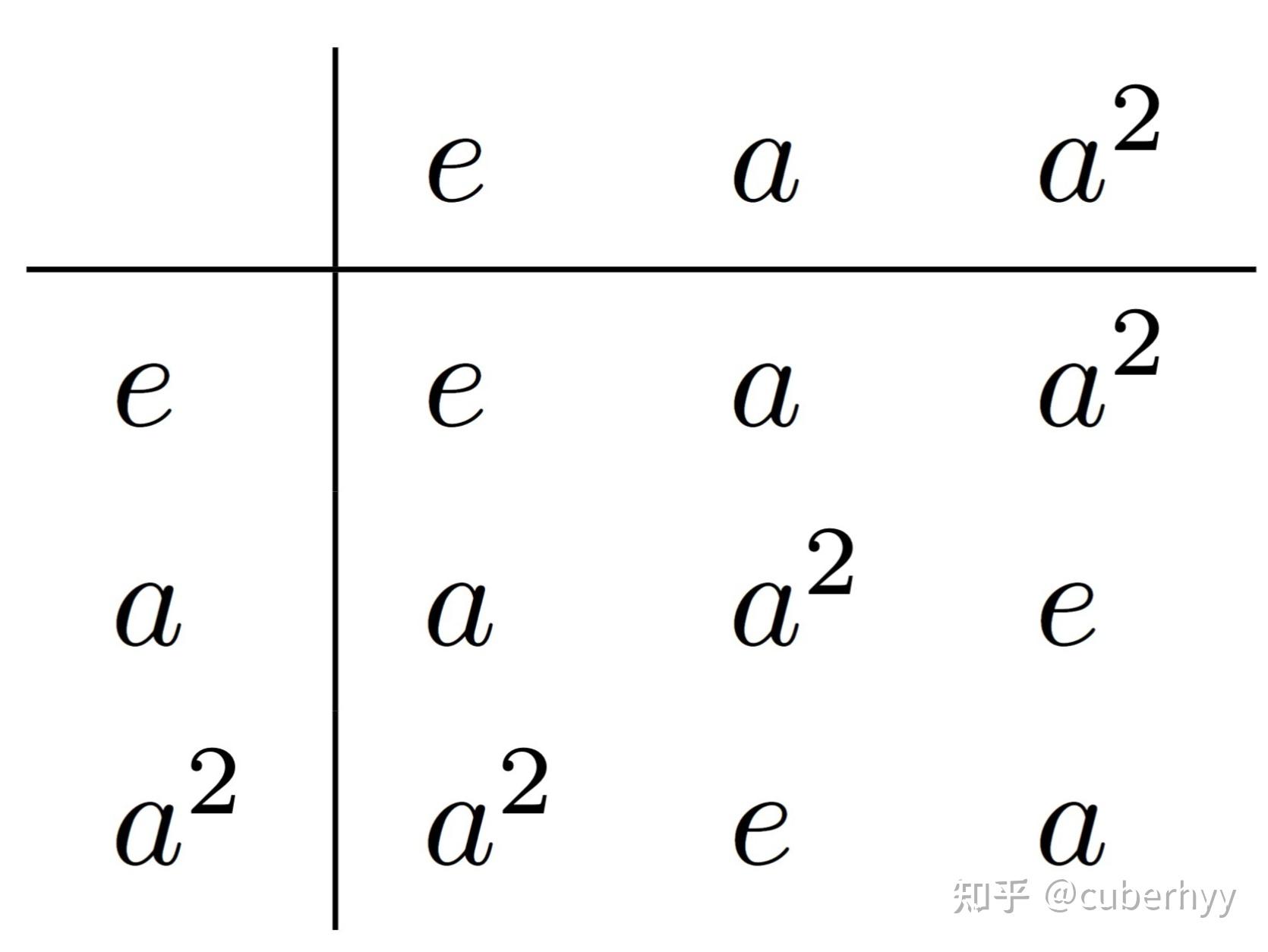
参考资料

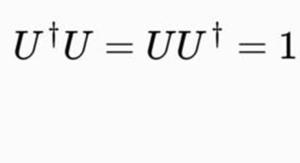


Moonshot回答
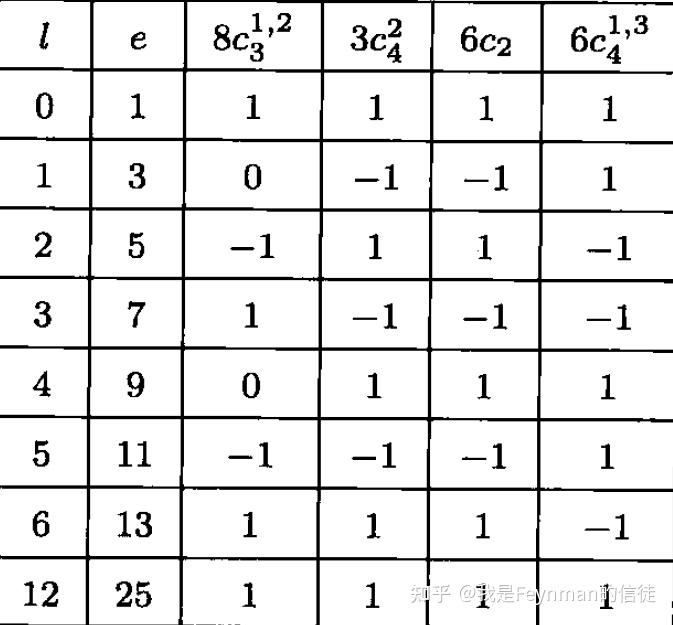
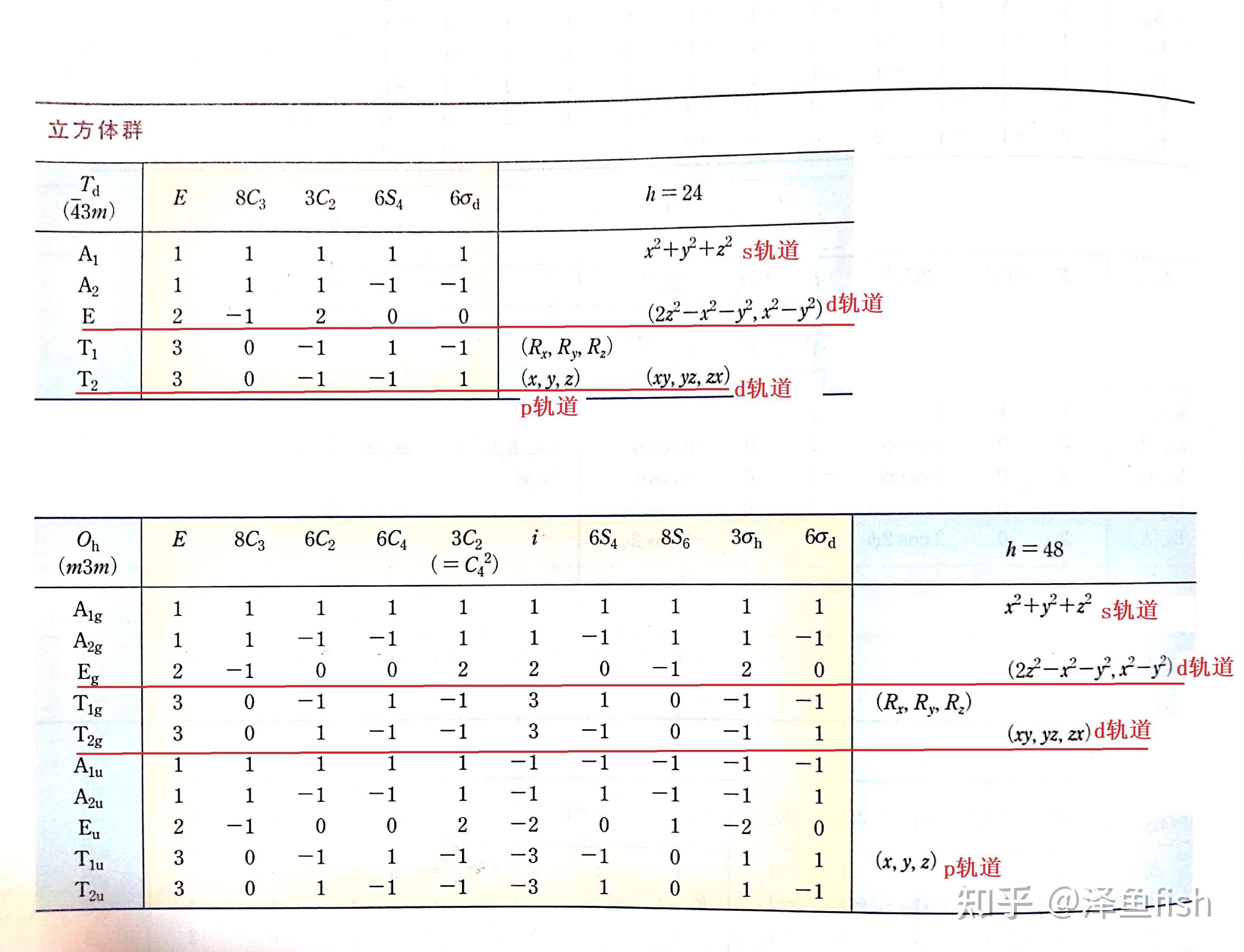
幺正算符在群论中扮演着重要的角色,尤其是在Hilb(H)群中的应用。根据搜索结果,幺正算符是希尔伯特空间的自同构,保持空间结构的不变性,例如线性叠加性、内积和拓扑性质。在群论中,一个给定希尔伯特空间H上的所有幺正算符组成了该空间的希尔伯特群,表示为Hilb(H)。这些算符满足U∗U = UU∗ = I,其中U∗是U的厄米转置,I是恒等算符。
幺正算符在量子力学中特别重要,因为它们代表量子态的演化,且这种演化是可逆的。在量子计算中,幺正变换用于实现量子比特的变换,保持量子信息的完整性。此外,幺正算符在量子信息理论中也扮演着关键角色,用于描述量子系统的演化和量子纠缠的性质。
总的来说,幺正算符在群论中的应用是多方面的,它们不仅在数学上有深刻的意义,还在物理学,尤其是量子力学和量子信息科学中有着重要的应用。