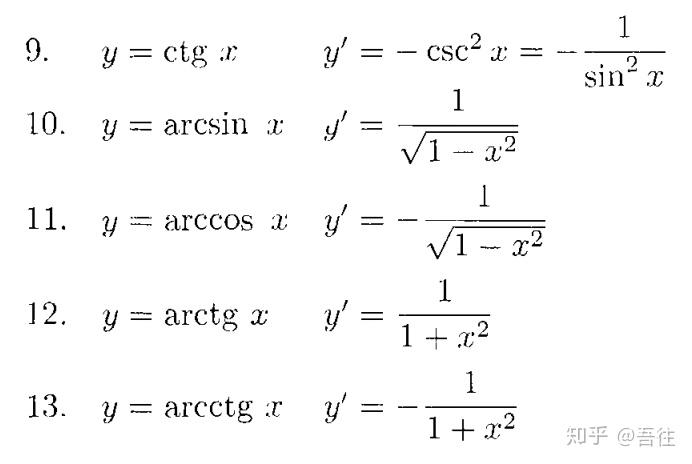如何理解并计算物理学中的外共变导数和曲率形式?
参考资料
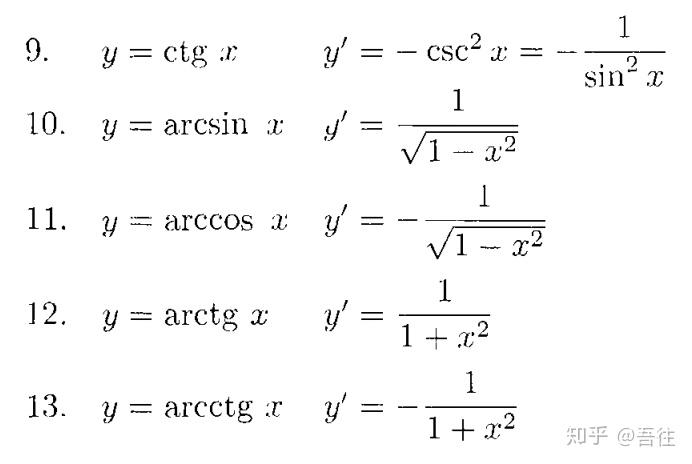



参考资料

Moonshot回答
在物理学中,外共变导数和曲率形式是描述物理系统几何性质的重要概念。外共变导数是流形上的微积分中一个非常有用的概念,它可能将利用主联络的公式化简。在物理学中,联络和外共变导数的概念被广泛应用于规范场论和广义相对论等领域。曲率形式则描述了流形的内在曲率,它与外共变导数密切相关,因为曲率形式可以通过外共变导数来定义。
外共变导数的计算通常涉及联络(connection)的概念,它描述了如何在流形上平行传输矢量或张量场。在规范场论中,联络可以与势能相关联,而外共变导数则与场的强度有关。曲率形式的计算则涉及到联络的导数,它描述了联络如何随流形上的位置变化。
在具体计算外共变导数和曲率形式时,通常需要使用到微分几何和张量分析的工具。例如,可以通过计算联络的协变导数来得到曲率形式,而外共变导数则涉及到联络对微分形式的作用。
从搜索结果中,我们可以看到一些关于外共变导数和曲率形式的计算方法和应用场景。例如,贝里曲率的计算公式广泛应用于数值计算,而曲率半径公式的推导则涉及到物理和数学的结合。这些内容可以帮助我们更深入地理解这些概念,并在实际问题中进行计算和应用。