参考资料

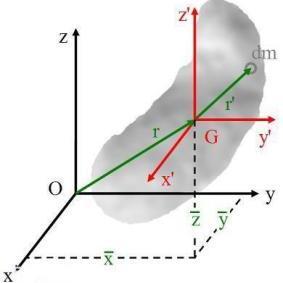
垂直轴定理在物理学中的应用主要体现在转动惯量的计算上。根据搜索结果，以下是一些具体的应用场景：

1. 薄片转动惯量计算：在直角坐标系中，如果薄片平行于两个坐标轴，并且已知薄片对于这两个轴的转动惯量，垂直轴定理可以用来计算薄片对于第三个垂直轴的转动惯量。这一应用在工程和物理问题中非常实用，因为它简化了转动惯量的计算过程。

2. 力学和工程问题：垂直轴定理在解决力学和工程问题时非常有用，尤其是在处理对称性问题时。例如，在计算复杂形状物体的转动惯量时，如果能够找到一对垂直轴使得物体对于这两条轴的转动惯量相等，那么可以利用垂直轴定理来简化计算。

3. 物理学教育：垂直轴定理也是物理学教育中的一个重要概念，如麻省理工学院的经典力学课程中就包含了垂直轴定理的应用，这有助于学生理解转动惯量的概念和计算方法。

4. 刚体转动惯量的简化计算：垂直轴定理可以推广到三度刚体的转动惯量计算中，从而简化了转动惯量的计算过程。这对于工程设计和物理分析非常重要，因为它减少了计算的复杂性。

总的来说，垂直轴定理是物理学中一个非常实用的工具，它在转动惯量的计算、力学问题解决、教育以及工程设计等领域都有广泛的应用。