阿伊姆霍兹方程在地震学中的具体应用是什么,如何利用它研究地震波?
参考资料

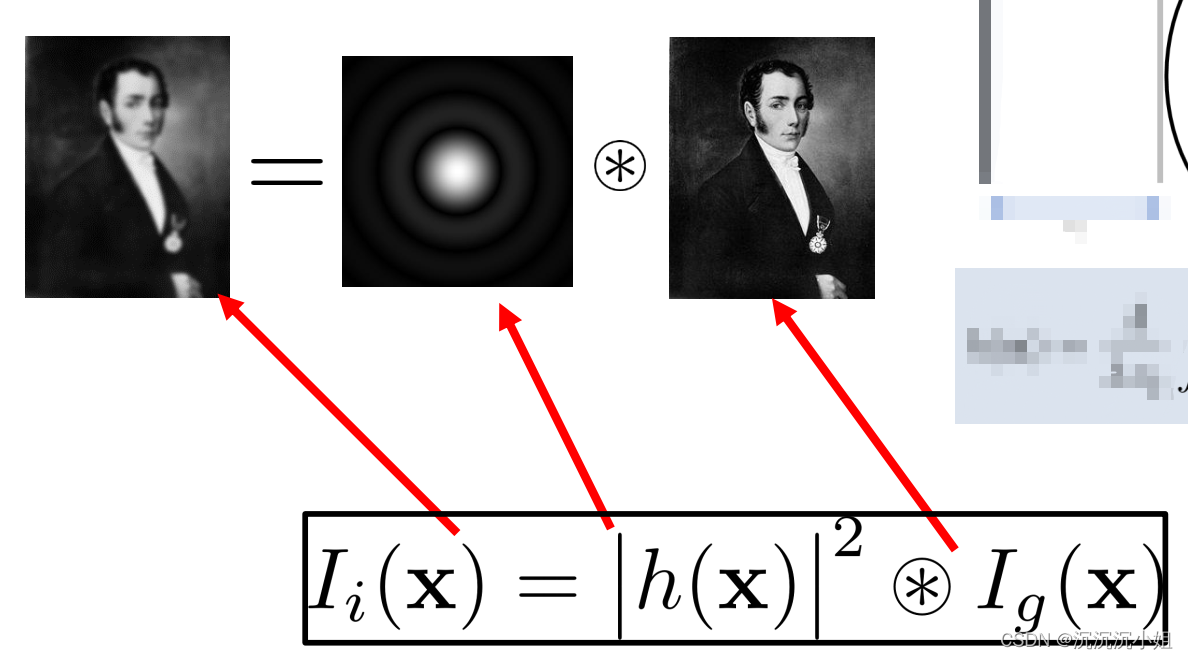
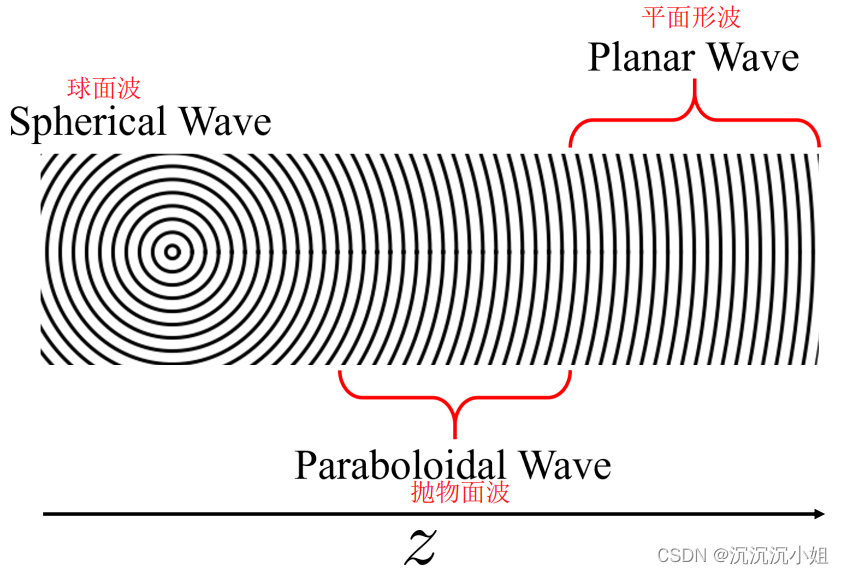
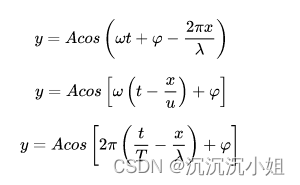
Moonshot回答
阿伊姆霍兹方程(Helmholtz方程)在地震学中的具体应用主要涉及地震波的模拟和研究。亥姆霍兹方程是描述波传播的偏微分方程,它在地震波的频域建模和全波形反演中发挥着重要作用。以下是一些具体的应用方式:
-
地震波的频域建模:通过求解亥姆霍兹方程,可以模拟地震波在不同地层介质中的传播。这种方法可以处理复杂的地下结构,如速度变化和边界条件,从而生成更准确的地震波传播模型。
-
全波形反演(FWI):在地震勘探中,全波形反演是一种重要的技术,用于从地震数据中提取地下结构信息。亥姆霍兹方程在此过程中用于模拟地震波的传播,帮助确定地下介质的物理属性,如密度和弹性模量。
-
地震波的散射问题:亥姆霍兹方程也用于研究地震波在遇到地下不规则结构时的散射行为。这对于理解地震波在复杂地质结构中的传播特性至关重要。
-
地震波的解析模型:亥姆霍兹方程可以用于构建地震波传播的解析模型,这对于理论研究和地震波传播的快速计算非常有用。
-
地震波的放大效应:在某些特殊地质结构,如河谷场地,亥姆霍兹方程可以帮助研究地震波的放大效应,这对于地震危险性评估和地震工程非常重要。
通过这些应用,亥姆霍兹方程为地震学家提供了一个强大的工具,以更好地理解和模拟地震波在地下介质中的传播行为。相关研究和应用的更多细节可以在以下链接中找到:
此外,以下是一些与地震波传播相关的图像,可以帮助直观理解亥姆霍兹方程在地震学中的应用:


