伽玛函数在数学中的主要应用是什么,它是如何定义的?
参考资料

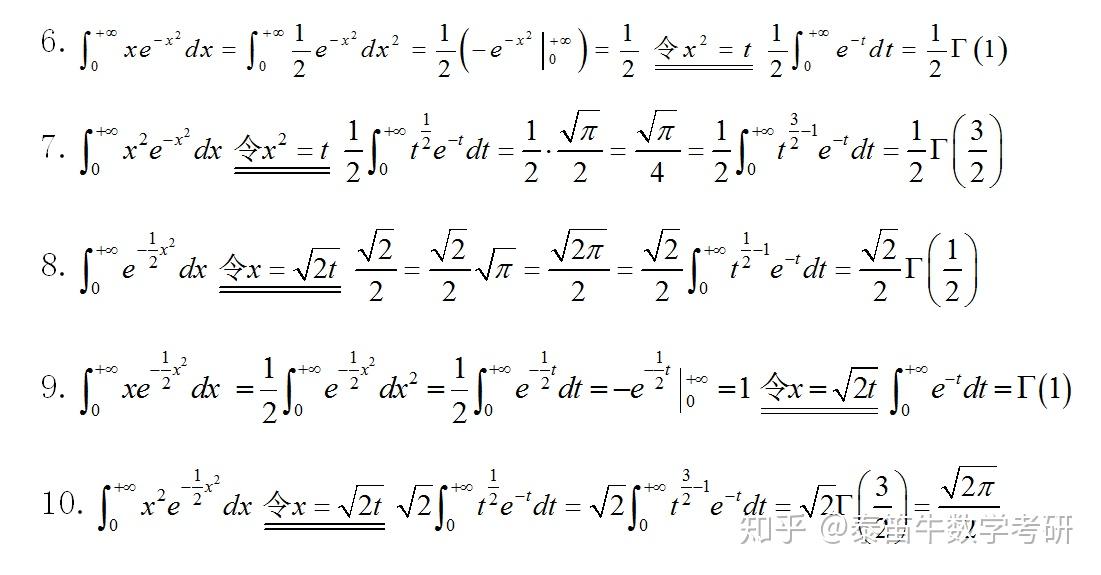
参考资料
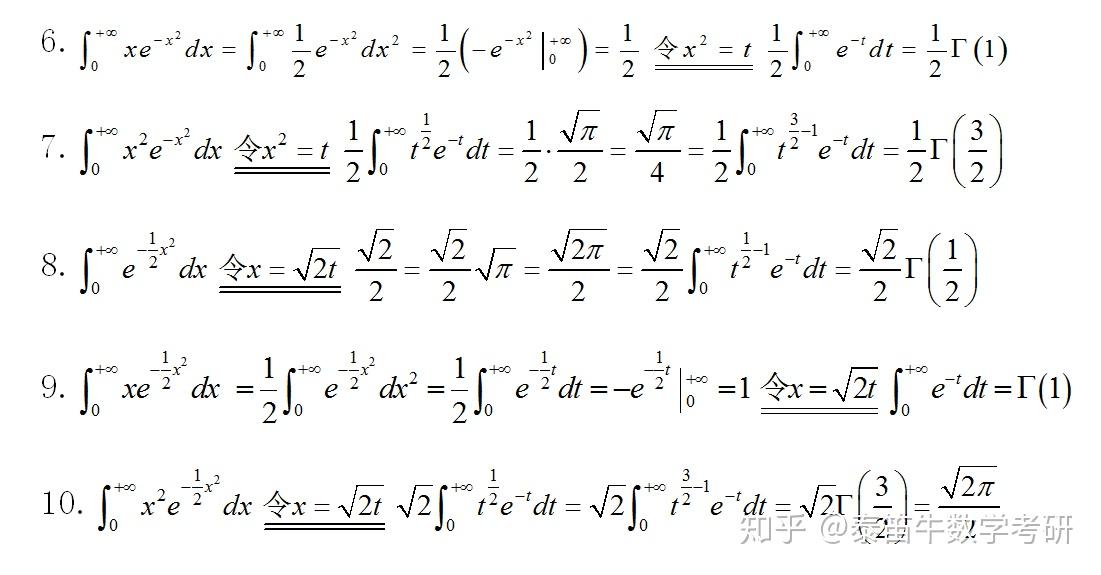

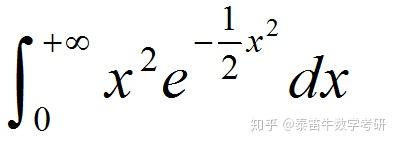
Moonshot回答
伽玛函数(Gamma函数)是阶乘函数在实数和复数域上的扩展。它主要定义为:
[ \Gamma(x) = \int_0^{+\infty} t^{x-1} e^{-t} dt ]
当( x )是非负整数时,伽玛函数的值等于( x-1 )的阶乘。对于复数,伽玛函数通过解析延拓原理定义在除去非正整数的整个复数域上。
伽玛函数在数学中有广泛的应用,包括但不限于:
- 分析学:在研究特殊函数和积分时经常用到。
- 概率论:用于定义伽玛分布和贝塔分布,这些分布在统计学中非常重要。
- 偏微分方程:在解某些类型的偏微分方程时会出现。
- 组合数学:在组合数学中,伽玛函数有助于解决涉及计数和排列的问题。
此外,伽玛函数还出现在n维球体的体积公式中,并且与贝塔函数(Beta函数)有密切联系,后者也用于计算积分。
以下是一些与伽玛函数相关的图像:

继续提问
相关问题
延展性在材料科学中是指什么性质,它是如何定义的?
达朗贝尔算符在Proca方程中有什么作用,它是如何定义的?
解释普朗克常数在量子力学中的重要性,它是如何定义的?
华雄在《三国演义》中展现了哪些英勇事迹,最终如何被击败?
请对比TOTO 智能马桶(标准款/300坑距)和九牧(ZS020)的参数,并分析它们的优缺点,然后打分推荐
博洛尼亚大学如何推动欧洲高等教育的改革?
《少女前线》游戏的主要玩法是什么?角色设定及背景故事如何与玩家互动?
武则天为何被传与安定思公主的夭折有关?
《地狱怪客2:金甲军团》的音乐是由谁负责创作的,他还创作过哪些知名电影的配乐?
耶路撒冷轻轨服务对沿雅法路的交通和商家有什么具体的影响?