参考资料

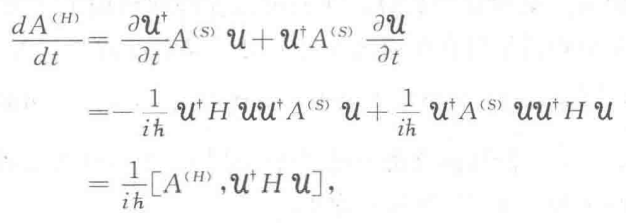

Moonshot回答
在薛定谔绘景中,量子态随时间的演化遵循薛定谔方程。量子系统的态矢量(或波函数)随着时间流易而演化,而像位置、自旋一类的对应于可观察量的算符则与时间无关。薛定谔方程是一个线性偏微分方程,它描述了量子态的时间演化。对于一个非相对论性的量子系统,时间无关的薛定谔方程形式如下:
[ \hat{H} \psi(x) = E \psi(x) ]
其中,(\hat{H}) 是哈密顿算符,代表系统的总能量,(\psi(x)) 是波函数,(E) 是能量本征值。波函数 (\psi(x)) 包含了关于系统的所有可能信息,而能量本征值 (E) 表示系统可能处于的量子态的能量。
时间依赖的薛定谔方程为:
[ i\hbar \frac{\partial}{\partial t} \Psi(x,t) = \hat{H} \Psi(x,t) ]
这里,(\Psi(x,t)) 是时间依赖的波函数,(i) 是虚数单位,(\hbar) 是约化普朗克常数。这个方程告诉我们,量子态随时间的变化率与哈密顿算符算出的系统能量有关。
在薛定谔绘景中,波函数 (\Psi(x,t)) 随时间变化,而算符保持不变。这与海森堡绘景不同,在海森堡绘景中,波函数不变,而算符随时间演化。薛定谔绘景因其直观性而在量子力学中被广泛使用,特别是在处理静态问题时。有关薛定谔绘景的更多信息,可以参考知乎上的相关讨论【量子力学】量子力学中为什么需要各种各样的绘景?和维基百科上的条目薛定谔绘景。
继续提问
相关问题
量子力学中的海森堡绘景和薛定谔绘景有什么区别和联系?
在海森堡绘景中,如何推导算符的时间演化方程?
不同级别行业的成本费用利润率变化反映了哪些潜在的经济或管理问题?
在互联网信息过剩的背景下,内容运营如何有效触达和保持用户的持续关注?
拉丁帝国是如何在君士坦丁堡建立并最终被拜占庭帝国收复的?
珍妮佛·拉梅(Jennifer Lame)是因为什么类型的电影剪辑工作而闻名的?
2000年代至今,古典音乐在现代社会中扮演了怎样的角色?
玄彬在演艺生涯中曾与哪些知名导演和演员有过合作,他们共同制作了哪些作品?
维多利亚女王在位期间,英国为何被称为“日不落帝国”?
阿方索五世的婚姻如何影响了他对卡斯提尔王位的觊觎?