参考资料
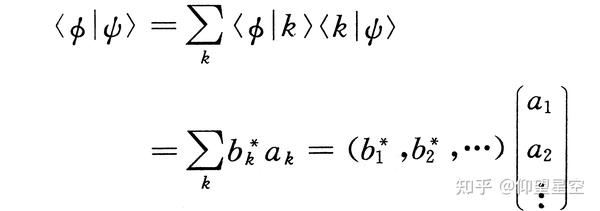
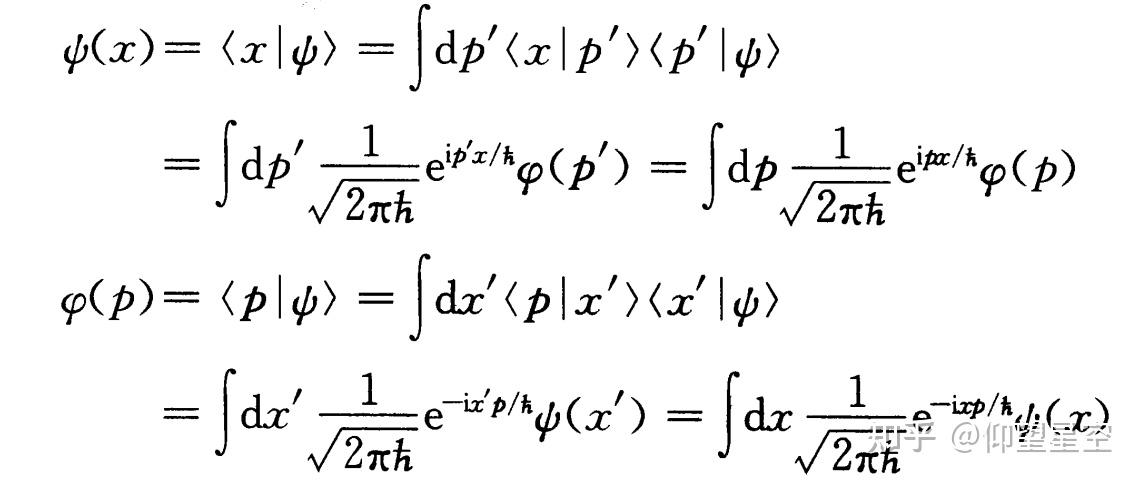
Moonshot回答
内积在狄拉克符号系统中具有几个重要的性质,这些性质有助于简化量子力学的表达和计算。以下是内积在狄拉克符号系统中的一些关键性质以及如何理解它们:
-
线性:内积对于第一个参数是线性的,对于第二个参数是共轭线性的。这意味着如果 ( |a\rangle ) 和 ( |b\rangle ) 是两个态矢量,( \alpha ) 和 ( \beta ) 是复数,那么 ( \langle a | (\alpha |b\rangle + \beta |c\rangle) = \alpha \langle a | b\rangle + \beta \langle a | c\rangle ) 和 ( (\alpha |a\rangle + \beta |b\rangle) |c\rangle = \alpha \langle a | c\rangle + \beta \langle b | c\rangle )。
-
共轭对称性:内积具有共轭对称性,即 ( \langle a | b\rangle = \langle b | a\rangle^* )。这意味着态 ( |a\rangle ) 和 ( |b\rangle ) 的内积是 ( |b\rangle ) 和 ( |a\rangle ) 内积的复共轭。
-
正定性:内积 ( \langle a | a\rangle ) 总是非负实数,并且仅当态矢量 ( |a\rangle ) 是零矢量时它才为零。这反映了量子力学中的物理态必须是归一化的。
-
完备性:在量子力学中,一组完备的正交基底可以表示任何态矢量。这意味着对于任何态矢量 ( |a\rangle ),都可以表示为基底态矢量的线性组合。
-
内积与概率幅:在量子力学中,内积 ( \langle a | b\rangle ) 表示从态 ( |a\rangle ) 到态 ( |b\rangle ) 的概率幅。其绝对值的平方 ( |\langle a | b\rangle|^2 ) 给出了从 ( |a\rangle ) 到 ( |b\rangle ) 的跃迁概率。
这些性质在量子力学中非常重要,因为它们提供了一种简洁而强大的方式去描述和计算量子态之间的相互作用和转换。通过狄拉克符号系统,我们可以更容易地处理量子态的叠加、测量和演化。