如何计算两个图像之间的均方误差(MSE)?
参考资料

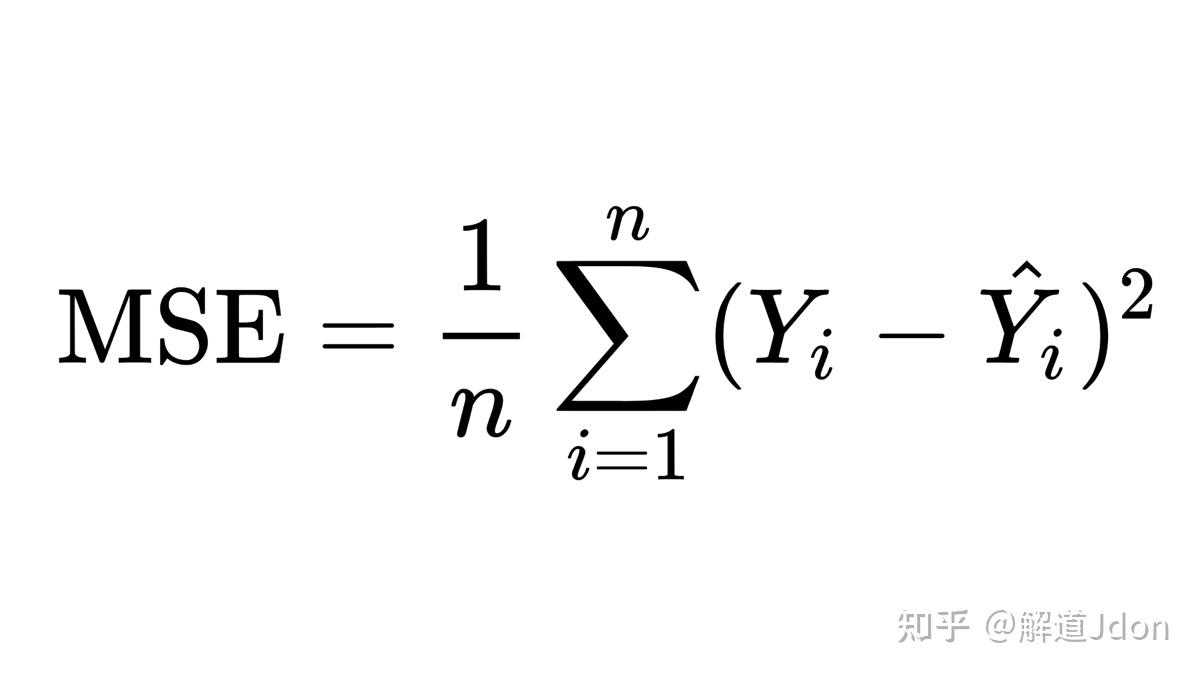
Moonshot回答
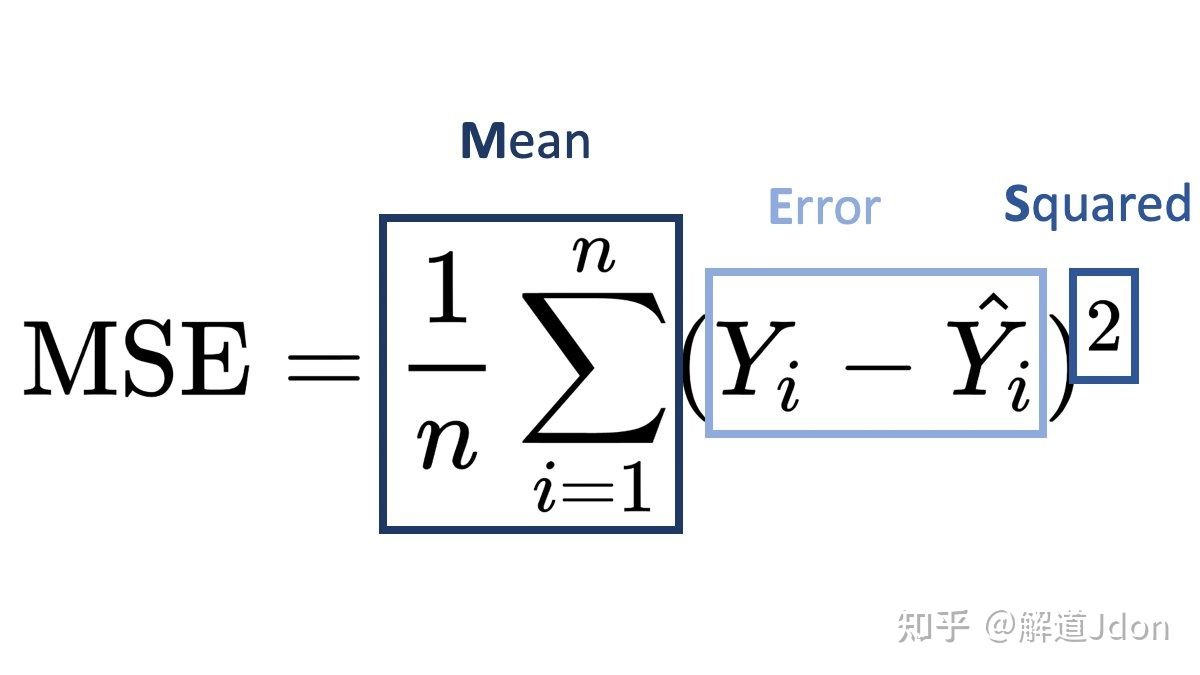
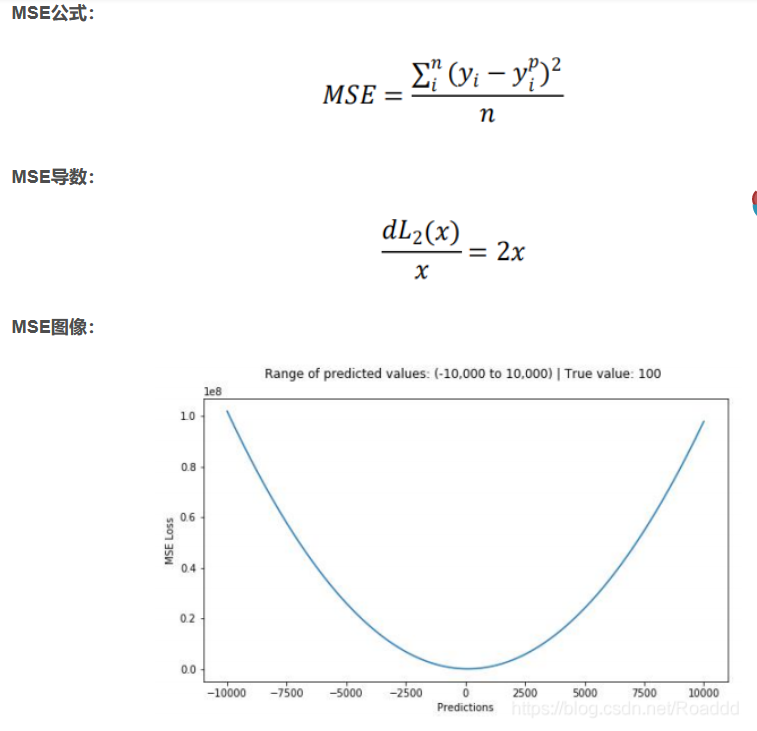
计算两个图像之间的均方误差(MSE)是一个衡量图像相似度的常用方法。MSE的计算公式如下:
[ MSE = \frac{1}{MN} \sum_{i=1}^{M} \sum_{j=1}^{N} (I(i, j) - K(i, j))^2 ]
其中:
- (M) 和 (N) 分别是图像 (I) 和 (K) 的行数和列数。
- (I(i, j)) 和 (K(i, j)) 分别是图像 (I) 和 (K) 在位置 ((i, j)) 的像素值。
MSE值越小,说明两个图像越相似。根据搜索结果,以下是一些计算MSE的代码示例:
- 使用Python和OpenCV库计算MSE:
import cv2
import numpy as np
# 读取两个图像
img1 = cv2.imread('image1.png')
img2 = cv2.imread('image2.png')
# 将图像转换为灰度图
img1_gray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
img2_gray = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# 计算MSE
mse = np.mean((img1_gray - img2_gray) ** 2)
print(f'MSE: {mse}')
- 使用MATLAB计算MSE:
% 读取两个图像
I = imread('image1.png');
K = imread('image2.png');
% 计算MSE
mse = immse(I, K);
disp(['MSE: ', num2str(mse)]);
这些代码示例展示了如何使用不同的编程语言和库来计算两个图像之间的MSE。通过比较MSE值,可以评估图像处理算法的效果或图像压缩技术的质量。图像处理之图像质量评价指标mse(均方误差) - Csdn博客 提供了更多关于MSE的详细信息和计算方法。