希尔伯特空间中的投影定理是什么,它在最小化距离问题中的应用是什么?
参考资料


Moonshot回答
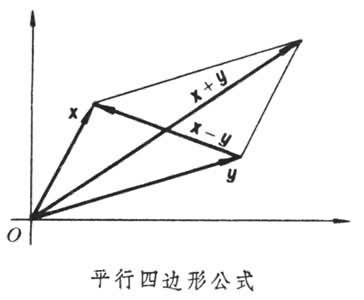
希尔伯特空间中的投影定理是泛函分析中的一个重要概念,它指出在希尔伯特空间中,对于任意向量b和闭子空间M,存在唯一的向量m0属于M,使得b和m0之间的距离最小化。这个距离是唯一的,并且向量b-m0垂直于子空间M。
在最小化距离问题中,投影定理的应用非常广泛。例如,在处理最小范数问题时,我们可以使用投影定理来找到子空间M中距离给定向量b最近的向量m0。这在优化问题中特别有用,因为它可以帮助我们找到最小化误差平方和的最优解。
此外,投影定理还与正交投影的概念密切相关。正交投影是极小化误差平方和问题的最优解,这在最小二乘问题中尤为重要。
以下是一些与希尔伯特空间中的投影定理及其在最小化距离问题中的应用相关的图像资源:
这些资源可以帮助我们更直观地理解投影定理及其在最小化距离问题中的应用。更多详细信息,可以参考知乎上的相关讨论[1],以及豆丁网上的学术文章[2]。