解释普朗克常数在量子力学中的重要性,它是如何定义的?
参考资料
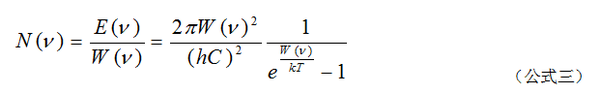
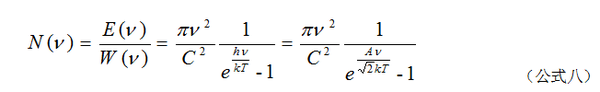
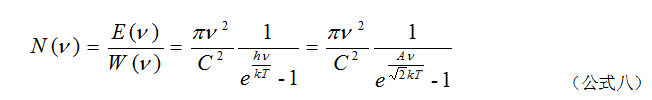
参考资料


Moonshot回答
普朗克常数(Planck constant),记为 ( h ),是量子力学中一个基本的物理常数,用以描述量子的大小。它的重要性在于,它揭示了能量在微观世界中的量子化性质。普朗克常数的值约为 ( 6.62607015 \times 10^{-34} ) 焦耳秒(J⋅s),它在量子力学的发展中起到了核心作用。
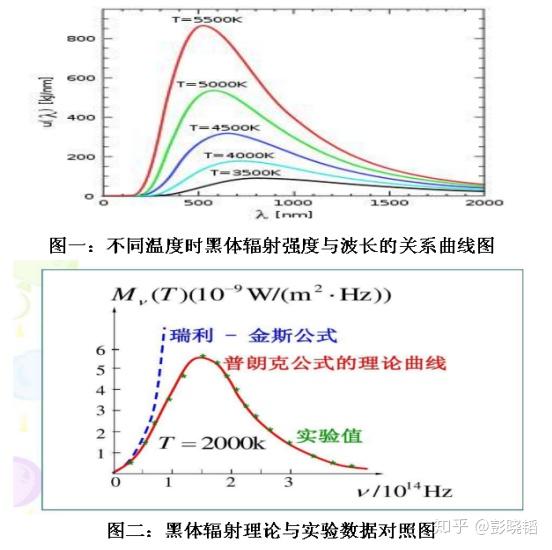
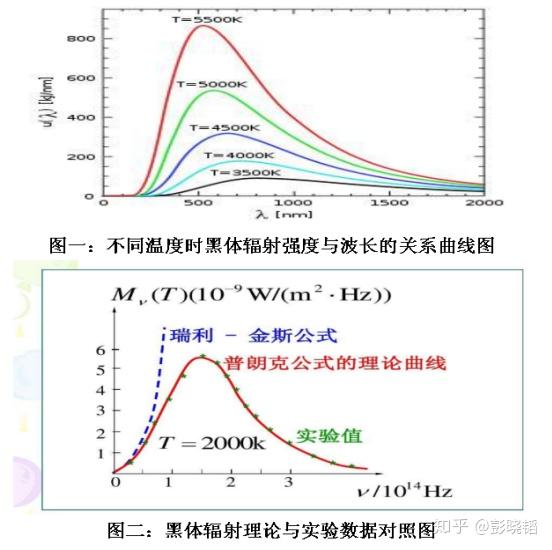
普朗克常数的定义来源于德国物理学家马克斯·普朗克在1900年的研究。普朗克在研究物体热辐射的规律时发现,只有假定电磁波的发射和吸收不是连续的,而是一份一份地进行的,计算的结果才能和实验结果相符。这样的一份能量被称为能量子(quantum),其大小等于普朗克常数乘以辐射电磁波的频率(( E = h\nu )),其中 ( \nu ) 为频率,( h ) 为普朗克常数。
普朗克常数在量子力学中的重要性体现在多个方面:
- 能量量子化:它表明能量的传输和吸收是量子化的,即以一定大小的能量子进行。
- 波粒二象性:普朗克常数是联系粒子的波动性质和粒子性质的关键,通过德布罗意假说,我们知道粒子的波长与其动量有关,而动量与能量通过普朗克常数联系。
- 不确定性原理:海森堡的不确定性原理指出,粒子的位置和动量不能同时被精确测量,这种不确定性与普朗克常数有关。
普朗克常数的发现标志着物理学从经典物理学向量子物理学的转变,是现代物理学的基石之一。通过引用搜狗百科的资料,我们可以了解到普朗克常数在量子力学中的重要角色,以及它是如何定义的。搜狗百科