参考资料

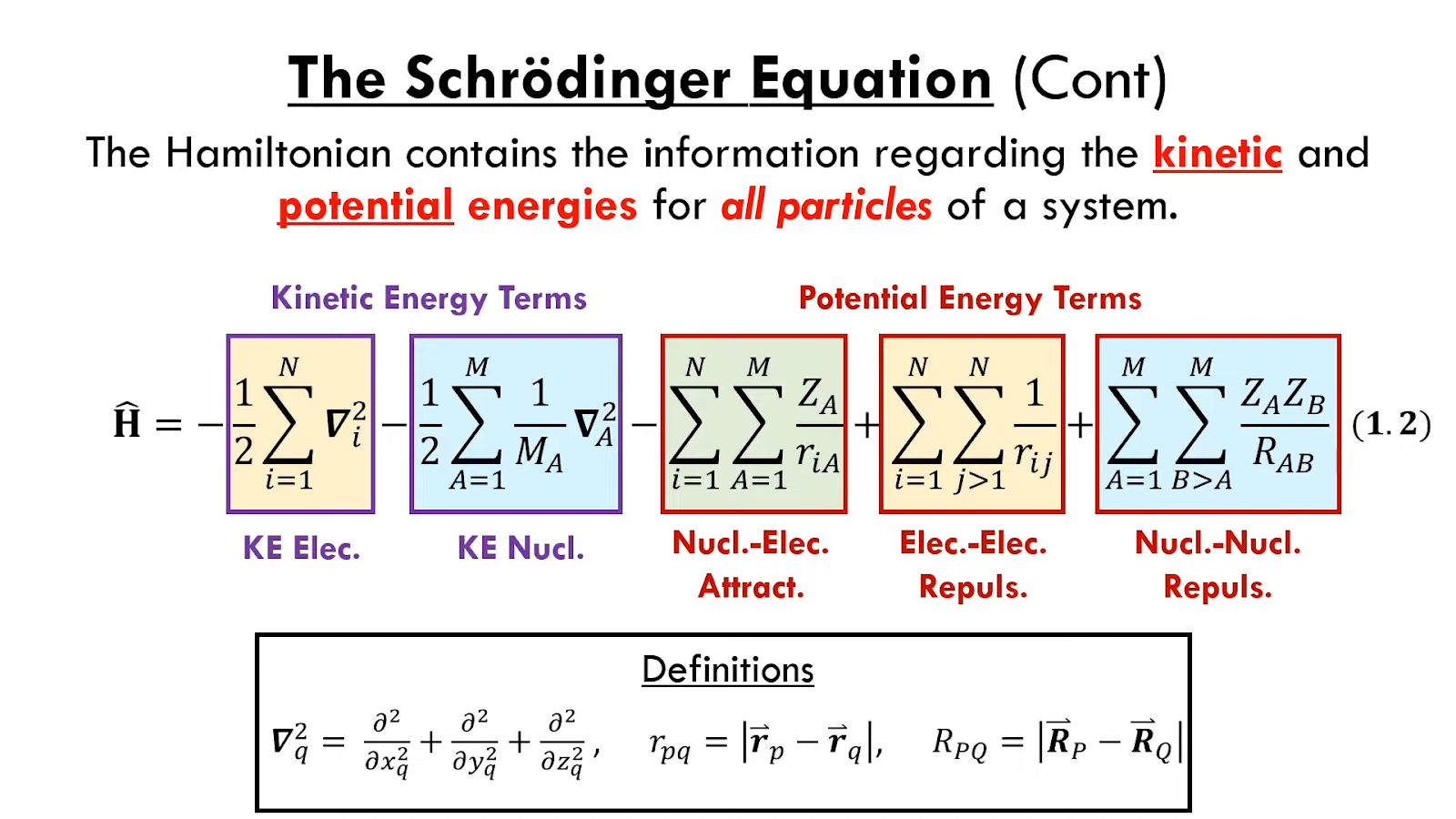
哈密顿算符在量子力学中扮演着核心角色，它代表系统的总能量，是描述量子体系状态演变和物理可观测量的关键算符。哈密顿算符的表达式通常包括动能和势能两部分，其形式可能因系统的不同而有所差异。例如，在非相对论性量子力学中，哈密顿算符可以表示为 ( \hat{H} = -\frac{\hbar^2}{2m}\nabla^2 + V(\mathbf{r}) )，其中 ( \nabla^2 ) 是拉普拉斯算符，( V(\mathbf{r}) ) 是势能函数，( \hbar ) 是约化普朗克常数，( m ) 是粒子的质量。

哈密顿算符在量子力学中的应用非常广泛，包括但不限于：

1. 薛定谔方程：哈密顿算符是构建薛定谔方程的基础，该方程是量子力学中描述物理系统状态随时间演化的基本方程。通过求解薛定谔方程，可以得到系统的波函数，进而计算出各种物理量的期望值。

2. 能量本征值问题：在量子力学中，哈密顿算符的特征值问题对应于系统的能量本征值问题。通过求解哈密顿算符的特征值和特征向量，可以得到系统的能级和相应的本征态。

3. 散射理论：在处理粒子散射问题时，哈密顿算符有助于分析入射粒子与靶粒子之间的相互作用，以及散射过程后粒子的最终状态。

4. 量子场论：在量子场论中，哈密顿算符被用来描述场的激发态和相互作用，是研究粒子产生和湮灭过程的重要工具。

5. 量子统计物理：哈密顿算符在量子统计物理中用于描述系统的热力学性质，如配分函数和熵，进而研究系统的热力学行为。

哈密顿算符不仅在理论物理中有着基础性的作用，还在各种实际应用中发挥着关键作用，如量子计算、量子信息处理、凝聚态物理、原子分子物理等领域。通过搜索结果，我们可以看到哈密顿算符在量子力学中的多方面应用，以及它如何与系统的动能和势能相关联。维基百科提供了关于哈密顿算符的详细信息，包括其数学表达式和物理意义。此外，通过查看相关的图像资源，可以获得对哈密顿算符在不同情境下应用的视觉理解。