参考资料
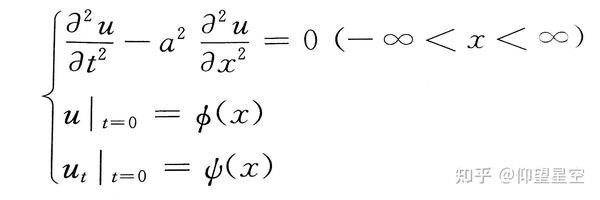
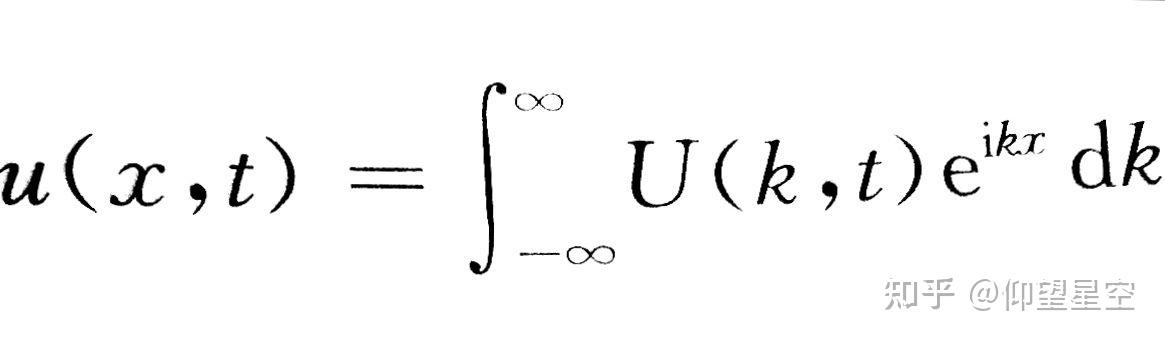
参考资料
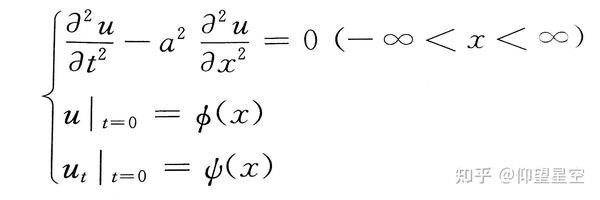
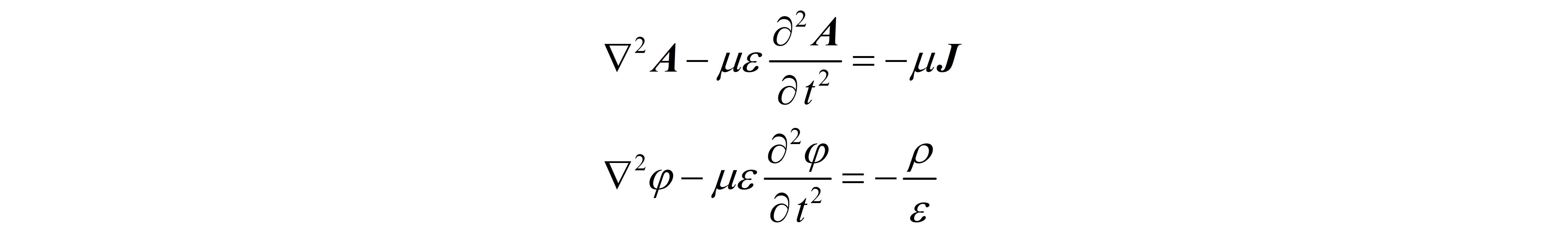
Moonshot回答
达朗贝尔算符在物理学中是一个重要的概念，特别是在狭义相对论、电磁学和波理论中。它定义为(\square = \nabla_{\mu} \nabla^{\mu} = \frac{1}{c^2} \frac{\partial^2}{\partial t^2} - \nabla^2)，其中(c)是光速，(\nabla^2)是三维空间下的拉普拉斯算子。这个算符以法国数学家和物理学家达朗贝尔命名，通常用于描述波动方程，例如在克莱因-戈尔登方程中。
在Proca方程中，达朗贝尔算符用于构建描述有质量矢量场的相对论性波动方程。Proca方程的一般形式是((\square + m^2)A^\mu = 0)，其中(m)是矢量场的质量，(A^\mu)是矢量势。这个方程在量子场论中非常重要，用于描述像W和Z玻色子这样的有质量粒子。
总的来说，达朗贝尔算符在Proca方程中的作用是提供一个相对论性框架来描述有质量的矢量场，这是理解某些基本粒子性质的关键。通过引用的搜索结果，我们可以更深入地了解达朗贝尔算符的定义和应用，以及它在Proca方程中的具体作用。
继续提问
相关问题
延展性在材料科学中是指什么性质，它是如何定义的？
解释普朗克常数在量子力学中的重要性，它是如何定义的？
伽玛函数在数学中的主要应用是什么，它是如何定义的？
Where's George? 网站上有多少美元钞票获得了五次以上的击，网站的纪录保持者是哪张钞票？
2018年各行业在视频广告、移动广告和程序化广告上的投入分别占整体支出的多少？
糙轴蕨与毛轴蕨在外形或生长习性上有什么具体区别？
成年人影视作品在娱乐和文化中的作用和影响有哪些？
电影《蝎子战士》中，费玉书最终采用什么功夫来破解蝎子功？
新建作业名称有什么限制，如何使用数字键和光标键输入名称？
《借物少女艾莉缇》中由宫崎骏负责剧本编写，他在剧本创作中有哪些值得注意的风格和特点？