向量叉积的模长与以参与运算向量为边的平行四边形面积有什么关系?
参考资料


Moonshot回答
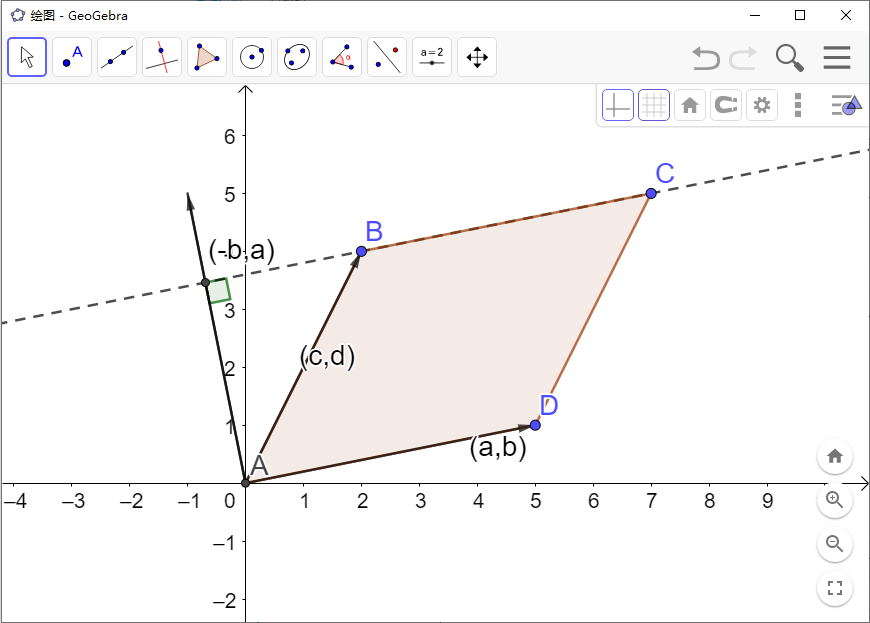
向量叉积的模长与以参与运算的向量为边的平行四边形面积有直接的关系。根据搜索结果,叉积的模长等于以这两个向量为边的平行四边形的面积。如果两个向量成直角,那么它们叉积的模长即为两者长度的乘积。此外,叉积的结果是一个向量,而非一个数,它表示两向量围成的平行四边形的面积(有向面积),这与行列式的几何意义保持一致。

在三维空间中,两个向量的叉乘结果是一个向量,其模长恰好等于了平面内这两个向量的外积。平行四边形的面积计算可以视为底乘以高,而叉积的模长正好提供了这个面积的量度。因此,叉积的模长与平行四边形面积的关系是它们相等,这体现了向量运算与几何形状面积之间的深刻联系。