请解释兰纳-琼斯势能公式中为何使用1/r^12和1/r^6项分别代表近距离排斥和远距离吸引作用?
参考资料
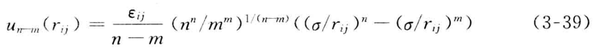


Moonshot回答
兰纳-琼斯势能公式(Lennard-Jones potential),又称L-J势或6-12势,是一个用来模拟两个电中性分子或原子间相互作用势能的数学模型。该公式由约翰·兰纳-琼斯于1924年提出,其表达式为:
[ V(r) = 4\varepsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right] ]
其中,( r ) 是两个原子之间的距离,( \varepsilon ) 是势能参数,( \sigma ) 是原子间距离的最小值(零点)。
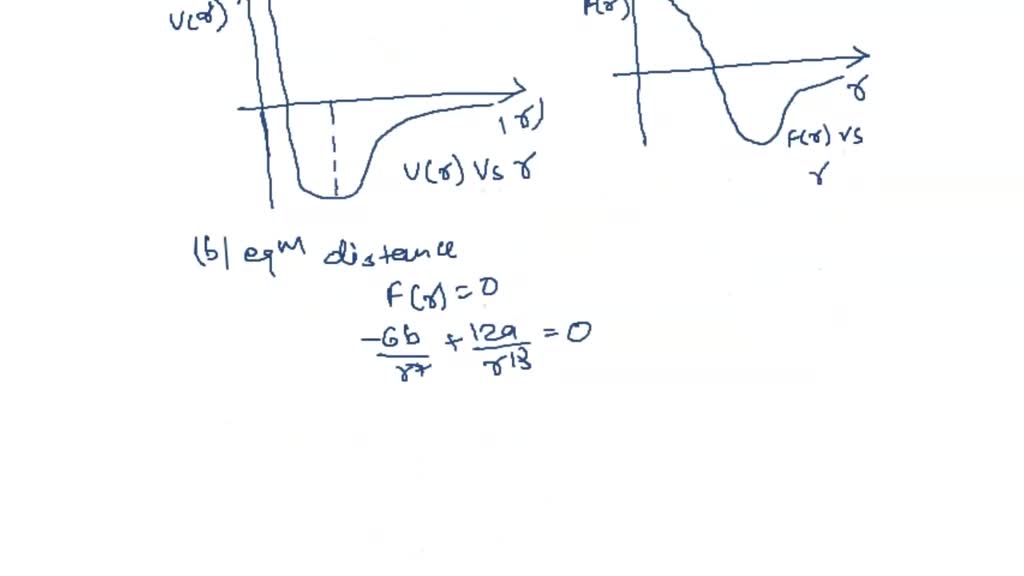
1/r^12项代表的是原子间在非常近的距离时的排斥作用。这种排斥力是由于原子的电子云开始重叠,导致强烈的电子间的排斥力。由于电子云重叠的概率与距离的立方成反比,因此排斥力与距离的-12次方成正比。
1/r^6项则代表的是原子间在稍远距离时的吸引作用。这种吸引力主要来源于瞬时偶极矩的产生,即一个原子的电子云瞬时偏离中心,导致正负电荷不均匀分布,从而吸引另一个原子。由于这种偶极矩的产生与原子间距离的平方成反比,因此吸引力与距离的-6次方成正比。
通过这种设计,兰纳-琼斯势能公式能够较好地模拟原子或分子间在不同距离下的相互作用,包括排斥和吸引两种力。这种模型在计算化学和材料科学中被广泛用于模拟分子间相互作用,尤其是在描述惰性气体分子间相互作用时非常精确。