参考资料

维度正则化在理论物理和实际应用中的价值体现在以下几个方面：

1. 量子场论中的计算：维度正则化是量子场论中处理发散积分的一种重要方法。物理学家使用维度正则化来计算费曼图的积分，这些积分的值是d的亚纯函数，其中d代表时空的维度。这种方法由Giambiagi、Bollini、Gerard 't Hooft和Martinus Veltman提出，它允许物理学家计算出有限值，从而在量子场论中得到有意义的结果。

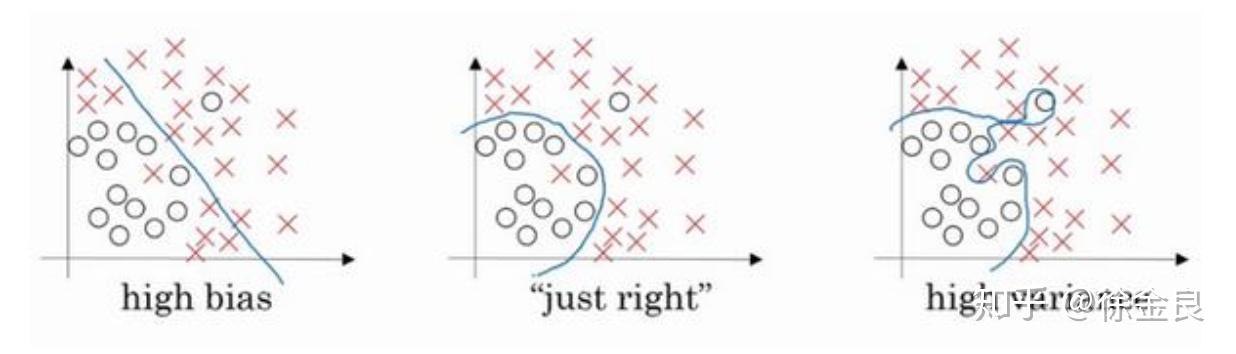
2. 控制模型复杂度：在机器学习领域，维度正则化有助于控制模型复杂度并提升泛化能力。通过在时间维度上进行正则化，可以在训练集上进行训练，并在统计上独立的验证集上进行评估。当模型在验证集上的性能不再提升时，可以提前停止训练，以防止过拟合。

3. 机器学习与统计物理的结合：机器学习在统计物理中的应用中，维度正则化的概念与物理学中的重正化群相似，有助于从微观规则中提取更精细尺度的表示。这种跨学科的结合为理论物理和机器学习领域带来了新的视角和方法。

4. 处理不适定的反问题：在数学物理中的反演问题，正则化算法通过寻求目标函数的极小值来提高搜索效率和准确度。正则化后的结果可以明显提高离精确解的准确度。

5. 量子引力研究：在现代量子引力领域，维度正则化有助于处理引力的量子化问题，保证了引力的背景无关性。这种方法有助于探索新的数学对象和数学性质，推动了物理数学领域的发展。

总的来说，维度正则化在理论物理中是处理量子场论中的发散问题的关键技术，在实际应用中，特别是在机器学习和统计物理的交叉领域，它有助于提高模型的泛化能力和处理复杂的反问题。这些应用展示了维度正则化在不同领域的广泛价值和深远影响。