配分函数与体系的内能、焓等宏观物理量之间有什么关系?
参考资料


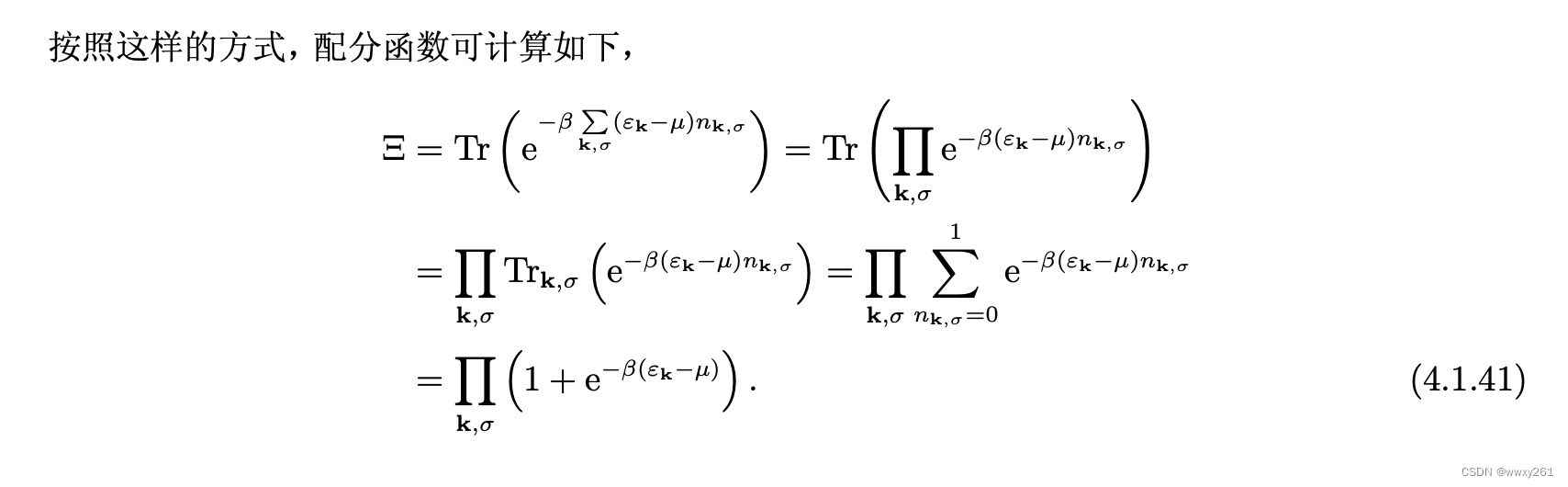

Moonshot回答
配分函数是统计物理学中一个重要的概念,它能够将微观物理状态与宏观物理量联系起来。通过计算配分函数,我们可以推导出体系的内能、焓、自由能等宏观物理量。
配分函数是生成函数,可以生成体系的内能、熵、焓、自由能等宏观量。内能(U)和焓(H)是热力学系统的状态函数,它们之间存在勒让德变换的关系。内能U与系统的能量状态有关,而焓H则包含了系统的内能加上其与外界的压力和体积的相互作用。具体来说,焓H等于内能U加上系统压力P与体积V的乘积(H = U + PV)。
从配分函数出发,我们可以得到系统的内能U和焓H的表达式。内能U可以通过对配分函数的自然对数求导数并乘以温度T来获得,即 (U = -\frac{\partial \ln Z}{\partial \beta} \beta^2),其中 (\beta = \frac{1}{kT}),k是玻尔兹曼常数,T是温度。而焓H可以通过对配分函数的自然对数求导数并乘以 (\beta) 来获得,即 (H = U + PV = -\frac{\partial \ln Z}{\partial \beta} \beta^2 + PV)。
此外,配分函数还可以帮助我们计算系统的其他热力学量,如自由能和熵。亥姆赫兹自由能F可以直接从配分函数中得到,而熵S可以通过内能U和亥姆赫兹自由能F的关系计算得出,即 (S = \frac{U - F}{T})。
综上所述,配分函数在统计物理学中扮演着至关重要的角色,它不仅能够将微观状态与宏观物理量联系起来,还能帮助我们计算和理解系统的内能、焓以及其他热力学量。通过配分函数,我们可以更深入地理解物质的宏观性质和微观行为之间的关系。