超对称理论如何帮助实现大统一理论中的耦合常数统一?
参考资料
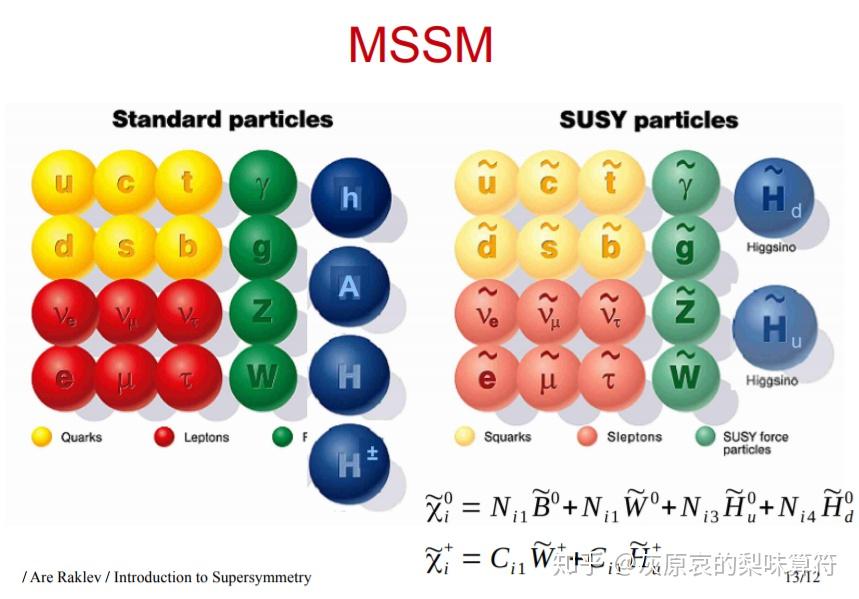

参考资料

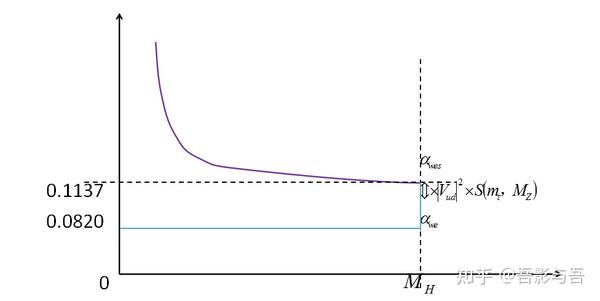
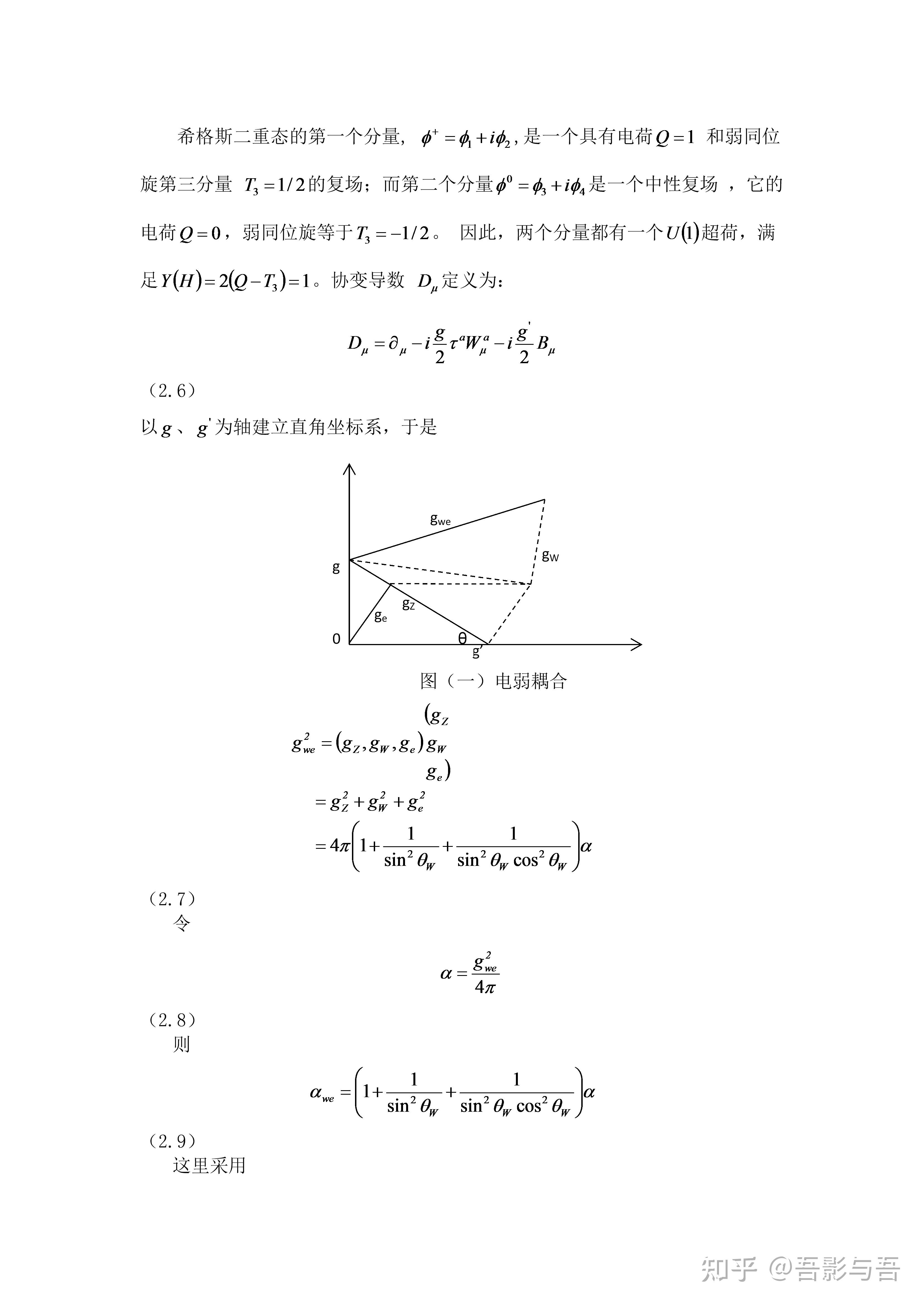

Moonshot回答
超对称理论(SUSY)在实现大统一理论(GUT)中耦合常数统一方面扮演了重要角色。在标准模型中,电磁、弱力和强力的耦合常数随着能量的增加而以不同的速率变化,这使得它们在低能量下无法统一。然而,通过引入超对称性,可以调整这些耦合常数的运行轨迹,使其在高能量下汇聚到一个点。
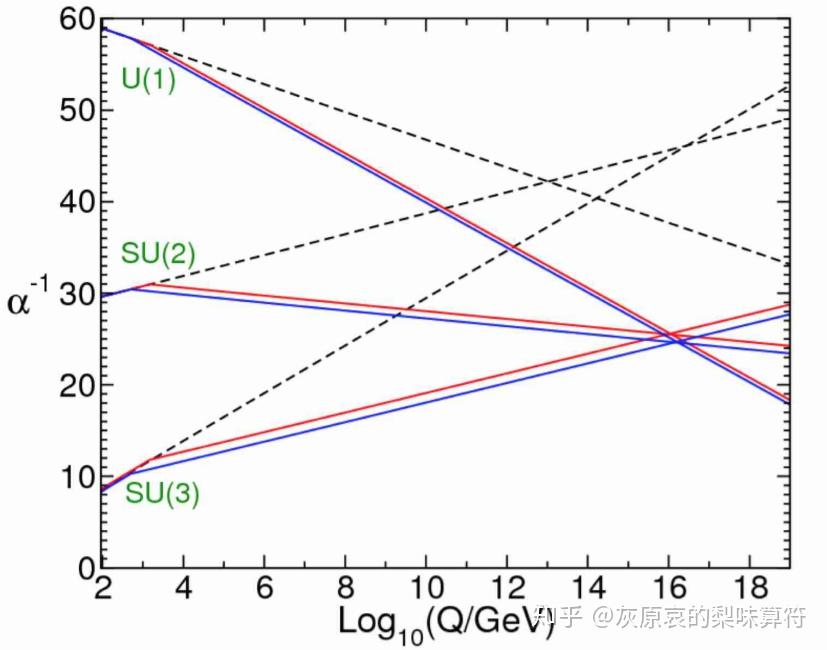
根据搜索结果,超对称理论的介入为大统一理论提供了新的希望。计算表明,在对标准模型进行超对称化后,所有这些耦合常数在高能下非常漂亮地汇聚到了一起。这一点大大增强了物理学家们对超对称的信心。此外,超对称模型能解决三个难题:在大统一理论尺度,它能够促使规范耦合常数收敛合一;它能够给出一个暗物质候选;并且有助于解决规范等级问题。
在超对称SU(5)大统一理论中,新的重整化群方程解出来的三条跑动曲线在误差范围内可以交于一点,这一点在高能下大约是10^16 GeV。这表明,超对称理论通过引入超对称伴子,对规范耦合常数的重整化群方程有额外的贡献,改变了方程的系数,从而实现了耦合常数的统一。
总的来说,超对称理论通过调整标准模型中粒子的属性和相互作用,为实现大统一理论中的耦合常数统一提供了一个可行的框架。尽管目前还没有实验证据直接支持超对称理论,但它仍然是理论物理学中一个非常活跃和有前景的研究方向。