参考资料

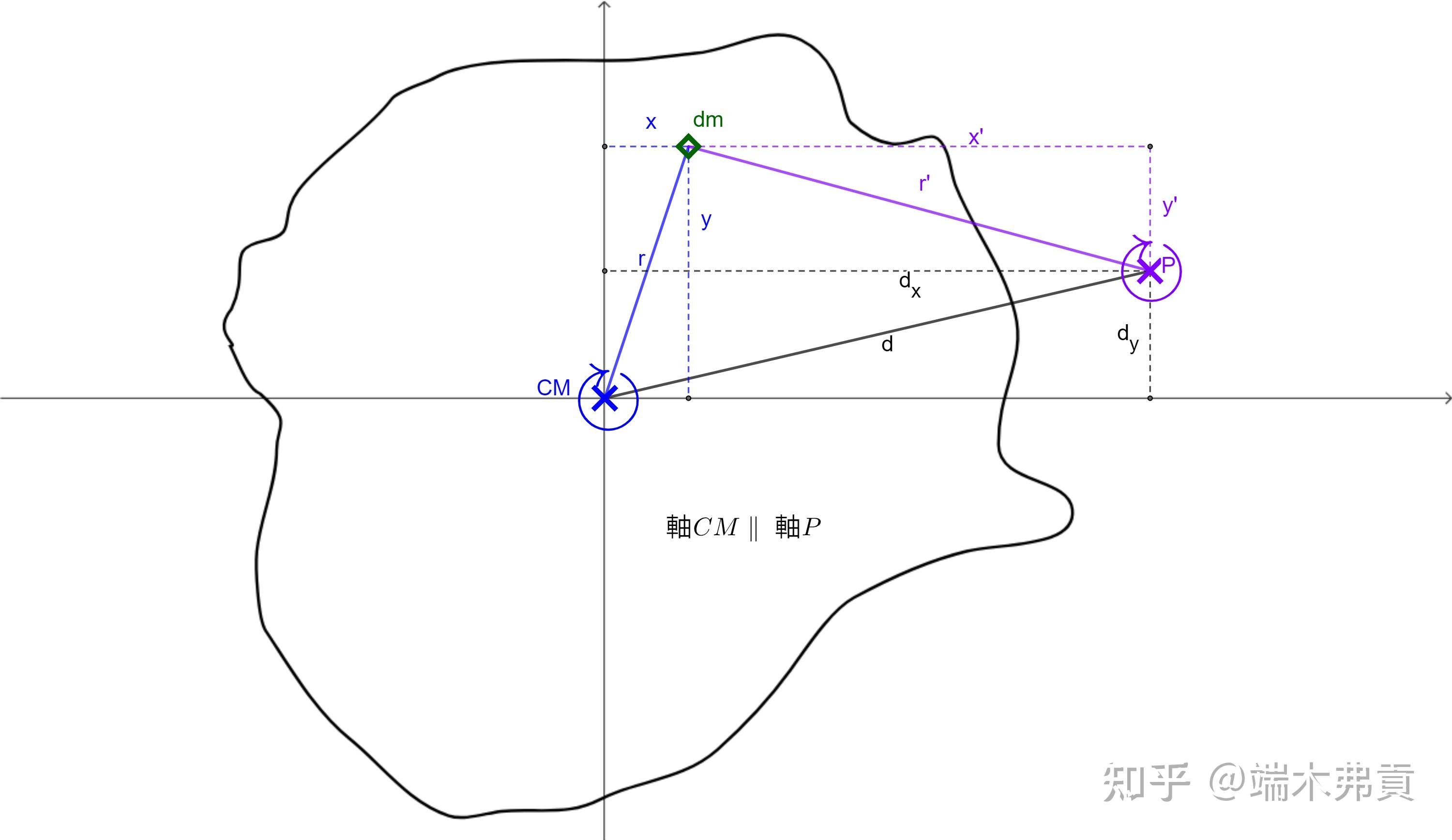
平行轴定理是计算复杂形状物体转动惯量的一个非常有用的工具。它允许我们通过已知的关于质心轴的转动惯量来计算关于另一平行轴的转动惯量。具体来说，如果我们知道一个物体关于通过其中心的轴（质心轴）的转动惯量 (I_{\text{cm}})，以及从质心轴到我们想要计算转动惯量的轴的距离 (d)，那么可以使用以下公式来计算新轴的转动惯量 (I)：

[ I = I_{\text{cm}} + Md^2 ]

其中 (M) 是物体的质量。

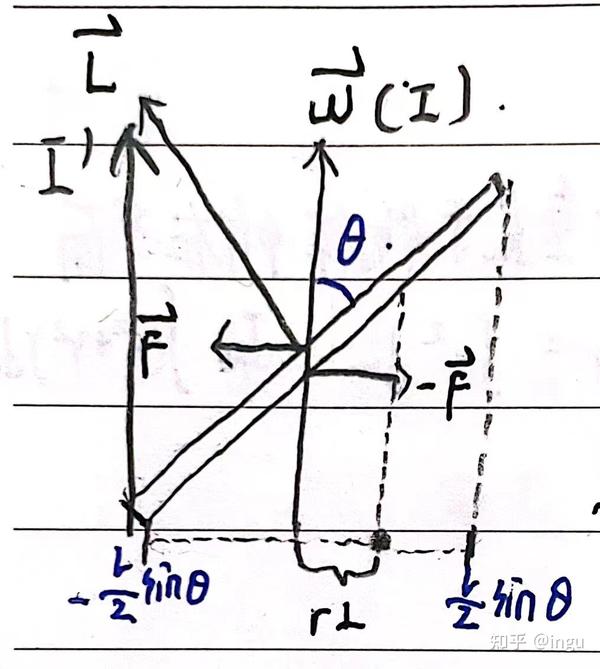
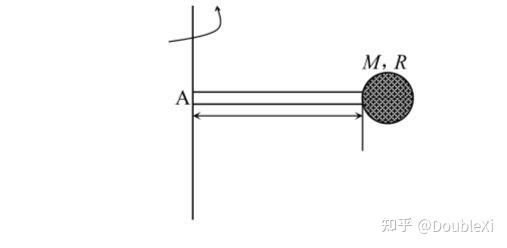
这个定理特别适用于那些直接计算转动惯量较为困难的复杂形状物体。例如，对于形状复杂、质量分布不均匀的刚体，通常采用实验方法来测定其转动惯量，如机械部件、电动机转子和枪炮的弹丸等。在验证转动惯量平行轴定理时，可以通过改变滑块的放置位置来测试不同质量分布对转动惯量的影响。

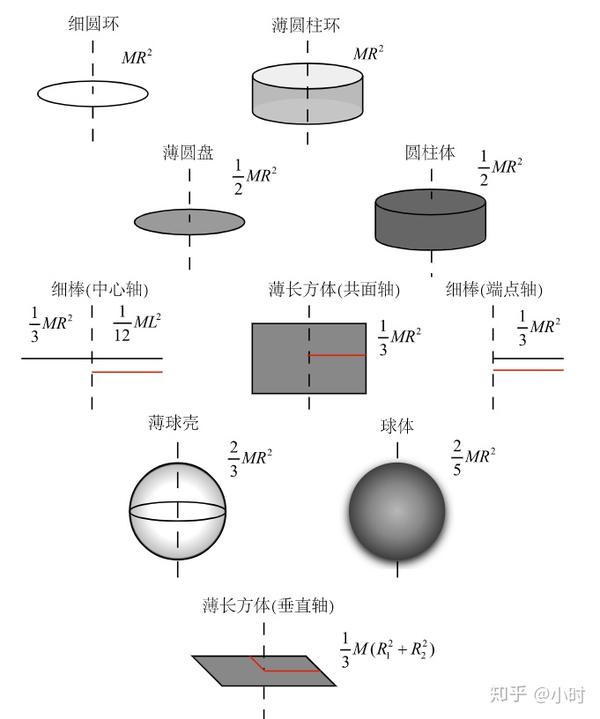
此外，平行轴定理、垂直轴定理和伸展定则等工具都可以用来求得许多不同形状的物体的转动惯量。这些定理提供了一种系统的方法来简化复杂形状物体转动惯量的计算过程。

图片来源：知乎

通过这种方式，我们可以更有效地理解和计算复杂形状物体的转动惯量，无论是在理论研究还是在工程应用中。