什么是L-S耦合,具体是如何应用在原子结构中的?
参考资料

Moonshot回答
L-S耦合,也称为Russell-Saunders耦合,是一种描述多电子原子中电子间相互作用的模型。在这个模型中,电子的轨道角动量(L)和自旋角动量(S)首先耦合成总角动量(J),然后再考虑电子间的相互作用。L-S耦合适用于较轻的原子,因为这些原子中电子间的静电斥力远大于自旋轨道相互作用。
在原子结构中,L-S耦合的应用包括:
-
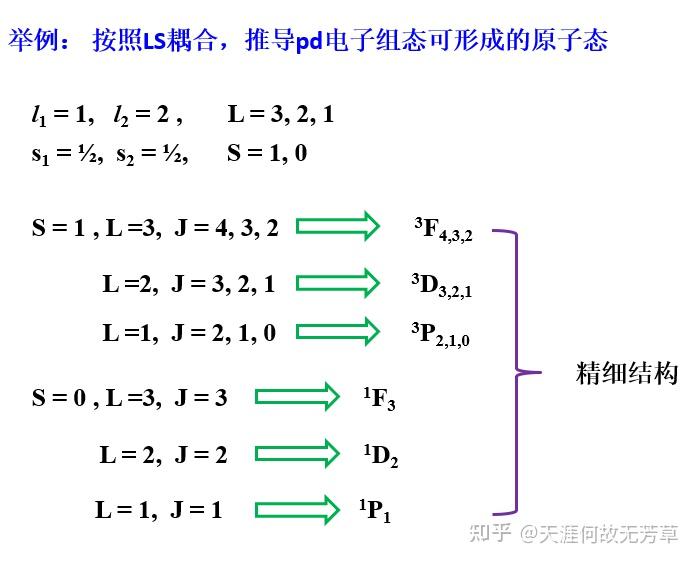
确定原子光谱项:通过L-S耦合,可以计算多电子原子的能级和光谱项,这在光谱学中非常重要。例如,两电子原子组态的能级计算可以通过L和S的投影到J矢量上来进行。
-
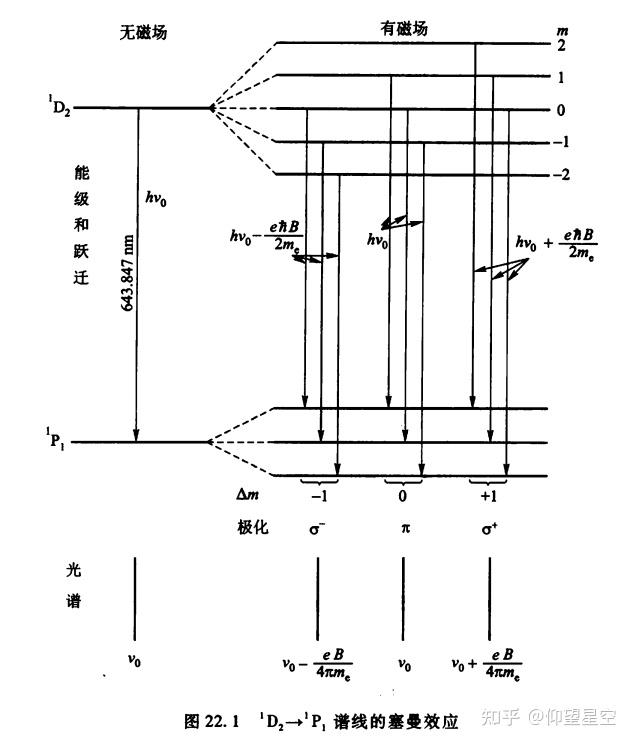
解释塞曼效应:在L-S耦合框架下,可以分析弱Zeeman效应,即在外部磁场作用下能级的分裂。这涉及到将L和S投影到J矢量上。
-
确定原子基态:存在一些简便方法来确定L-S耦合下原子的基态,这对于理解原子的电子壳层结构至关重要。
-
计算精细结构能量:在较轻的原子中,精细结构能量的差异可以通过L-S耦合来计算,而在较重的原子中,则可能需要使用jj耦合。
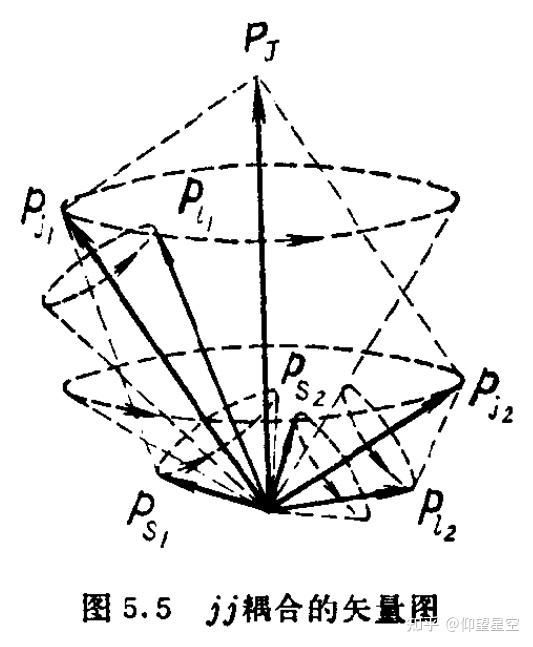
L-S耦合与jj耦合不同,后者适用于较重的原子,其中自旋轨道相互作用更为显著。在L-S耦合中,好量子数为L、S和J,而在jj耦合中,好量子数为j1、j2和J。
 LS耦合示意图
LS耦合示意图
通过这种方式,L-S耦合提供了一种理解和计算多电子原子结构和光谱性质的有效方法。更多详细信息可以参考相关学术文章和资源,例如知乎上关于LS耦合和jj耦合的讨论,以及关于L-S耦合法确定多电子组态原子光谱项的计算机实现的研究。