勒贝格积分和黎曼积分的区别是什么,为什么勒贝格积分更为广泛应用?
参考资料


参考资料


Moonshot回答
勒贝格积分和黎曼积分是两种不同的积分理论,它们在定义和应用上有显著的区别。以下是它们的主要区别以及勒贝格积分为什么被更广泛应用的原因:
-
定义方式不同:
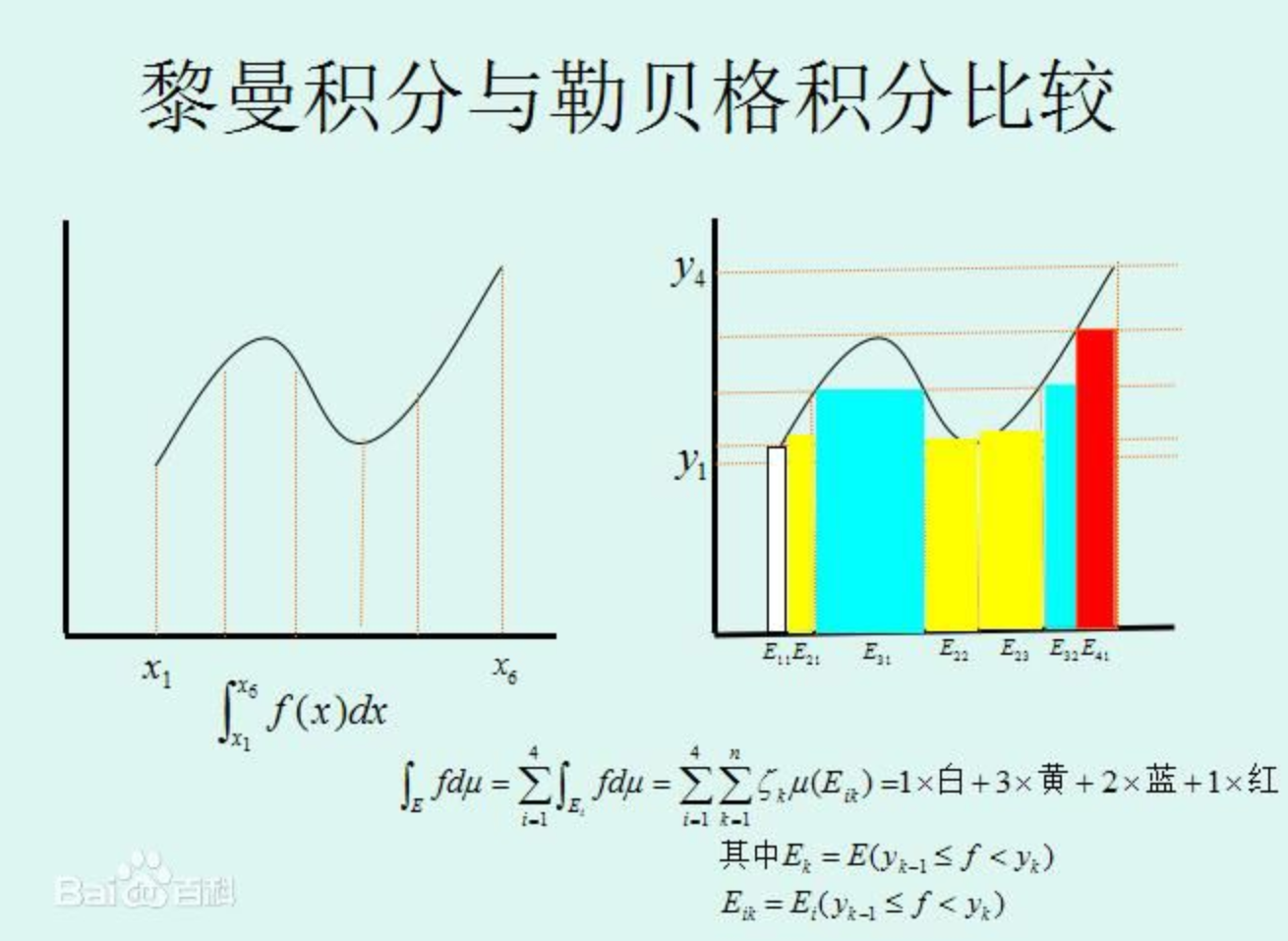
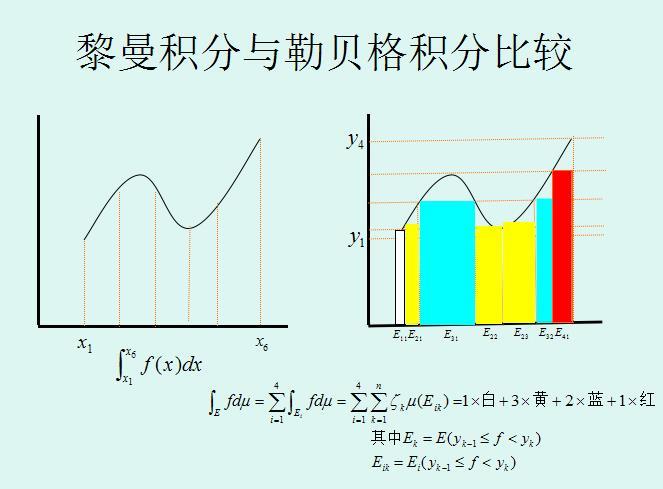
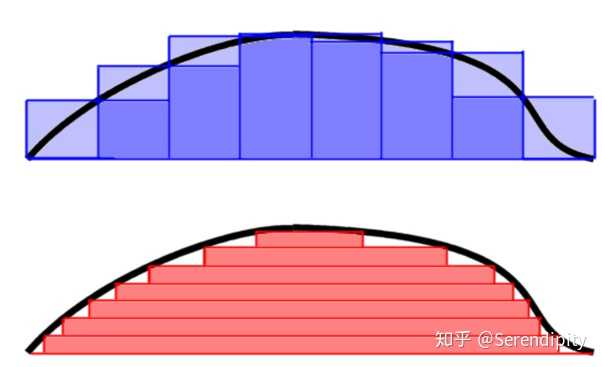
- 黎曼积分是基于定义域划分的,通过将定义域分割成小区间,然后对每个小区间的函数值进行求和来近似积分值。
- 勒贝格积分则是基于值域划分的,它通过对函数的值域进行划分,然后计算每个区间的测度和函数值的乘积来求和。
-
可积函数的范围:
- 黎曼积分主要适用于连续函数,对于不连续的函数,黎曼积分可能无法定义或者计算。
- 勒贝格积分则可以处理更广泛的函数,包括那些黎曼积分无法处理的函数,如某些不连续的函数。
-
收敛性质:
- 勒贝格积分具有更好的收敛性质,例如勒贝格控制收敛定理,它允许在一定条件下交换极限和积分的顺序。
- 黎曼积分则没有这样的性质,这限制了它在处理极限和积分交换问题时的应用。
-
应用范围:
- 勒贝格积分在调和分析、偏微分方程、泛函分析等领域有广泛的应用,它能够更容易地处理二重积分、曲面积分等问题。
- 黎曼积分虽然在技术上存在某些不足,但勒贝格积分实际上是黎曼积分的扩展,每个黎曼可积函数都是勒贝格可积的,并且在两者都有定义时积分值是一致的。
-
抽象程度:
- 勒贝格积分更加抽象,它建立在测度论的基础上,这使得它在数学分析中具有更强大的工具和更广泛的应用。
- 黎曼积分相对直观,但这种直观性在处理复杂问题时可能成为限制。
综上所述,勒贝格积分因其在定义、可积函数范围、收敛性质以及应用范围上的优势,被更广泛地应用于现代数学的各个领域。尽管它更抽象,但这些抽象概念为解决复杂的数学问题提供了强大的工具。
继续提问
相关问题
朝鲜地震局在进行地震监测和预测方面采用了哪些技术和设备?中国对其有哪些具体支持?
花是如何独自养育两只狼孩子的,她在乡下的生活条件有哪些显著改变?
台北市在1935年的人口占台湾总人口的比例是多少?
夷陵之战对三国格局产生了哪些深远影响?
和泉雅子的冒险家经历中除了登顶北极,她还有哪些著名的探险活动?
威廉·詹宁斯·布莱恩在1896年大选失败后,为何成为美国历史上首位向胜选者发贺电的总统候选人?
在穆斯林征服西西里期间,拜占庭帝国为何未能有效援助被围困的叙拉古?
哥特式文学的代表作品有哪些?它们如何通过神秘与恐怖的气氛吸引读者?
土地改良项目的费用是如何计算的,哪些改良项目会被归入单独的土地改良账户?
米基·洛克在电影中的编剧作品有哪些?